题目内容
17.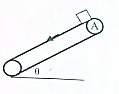 如图所示,倾角为θ的传送带,以v0的恒定速度按图示方向运动.已知传送带上下两端相距L,今将一与传送带间动摩擦因数为μ的滑块A静止放于传送带上端,求A从上端运动到下端的时间t.
如图所示,倾角为θ的传送带,以v0的恒定速度按图示方向运动.已知传送带上下两端相距L,今将一与传送带间动摩擦因数为μ的滑块A静止放于传送带上端,求A从上端运动到下端的时间t.
分析 对物体受力分析,利用牛顿第二定律和运动学公式求的加速度,关键是讨论L的大小和摩擦力的大小
解答 解:对物体受力分析可知
(1)当mgsinθ<μmgcosθ时,物体在斜面上的加速度为a=$\frac{mgsinθ+μmgcosθ}{m}=gsinθ+μgcosθ$
达到共同速度所需时间为t=$\frac{{v}_{0}}{gsinθ+μgcosθ}$
此时下滑的位移为x=$\frac{1}{2}a{t}^{2}=\frac{{v}_{0}^{2}}{2(gsinθ+μgcosθ)}$
当L≤x时经历的时间由公式L=$\frac{1}{2}a{t}^{2}$可得t=$\sqrt{\frac{2L}{gsinθ+μgcosθ}}$
当L≥x时,达到共同速度之后物体继续随传送带做匀速运动经历的时间为t$′=\frac{L-x}{{v}_{0}}=\frac{L}{{v}_{0}}-\frac{{v}_{0}}{2(gsinθ+μgcosθ)}$
故经历的总时间为${t}_{总}=t+t′=\frac{L}{{v}_{0}}+\frac{{v}_{0}}{2(gsinθ+μgcosθ)}$
(2)当mgsinθ>μmgcosθ时,物体在斜面上的加速度为a=$\frac{mgsinθ+μmgcosθ}{m}=gsinθ+μgcosθ$
达到共同速度所需时间为t=$\frac{{v}_{0}}{gsinθ+μgcosθ}$
此时下滑的位移为x=$\frac{1}{2}a{t}^{2}=\frac{{v}_{0}^{2}}{2(gsinθ+μgcosθ)}$
当L≤x时经历的时间由公式L=$\frac{1}{2}a{t}^{2}$可得t=$\sqrt{\frac{2L}{gsinθ+μgcosθ}}$
当L≥x时,达到共同速度之后物体继续加速运动,加速度为a′$\frac{mgsinθ-μmgcosθ}{m}=gsinθ-μgcosθ$
继续加速所需时间为t″,则$L-x={v}_{0}t″+\frac{1}{2}a′t{″}^{2}$
解得t″=$\frac{-2{v}_{0}+\sqrt{{4v}_{0}^{2}-8(gsinθ-μgcosθ)(\frac{{v}_{0}^{2}}{2(gsinθ+μgcosθ)}-L)}}{2(gsinθ-μgcosθ)}$
故下滑总时间为${t}_{总}=t+t″=\frac{{v}_{0}}{gsinθ+μgcosθ}+\frac{-2{v}_{0}+\sqrt{{4v}_{0}^{2}-8(gsinθ-μgcosθ)(\frac{{v}_{0}^{2}}{2(gsinθ+μgcosθ)}-L)}}{2(gsinθ-μgcosθ)}$
答:A从上端运动到下端的时间t为$\sqrt{\frac{2L}{gsinθ+μgcosθ}}$或$\frac{L}{{v}_{0}}+\frac{{v}_{0}}{2(gsinθ+μgcosθ)}$或$\frac{{v}_{0}}{gsinθ+μgcosθ}+\frac{-2{v}_{0}+\sqrt{{4v}_{0}^{2}-8(gsinθ-μgcosθ)(\frac{{v}_{0}^{2}}{2(gsinθ+μgcosθ)}-L)}}{2(gsinθ-μgcosθ)}$.
点评 解决本题的关键理清木块的运动情况,结合牛顿第二定律和运动学公式求解

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案| A. | 80N、70N、20N | B. | 6N、9N、30N | C. | 10N、11N、20N | D. | 21N、4N、6N |
| A. | 原子中存在着带负电的电子 | |
| B. | 正电荷在原子内是均匀分布的 | |
| C. | 原子只能处于一系列不连续的能量状态中 | |
| D. | 原子的正电荷和绝大部分质量集中在一个很小的核上 |
 如图所示,质量为m的足球在水平地面的位置1被踢出后落到水平地面的位置3,在空中达到的最高点位置2的高度为h,已知重力加速度为g,下列说法中正确的是( )
如图所示,质量为m的足球在水平地面的位置1被踢出后落到水平地面的位置3,在空中达到的最高点位置2的高度为h,已知重力加速度为g,下列说法中正确的是( )| A. | 足球由1运动到2的过程中,重力做的功为mgh | |
| B. | 足球由1运动到3的过程中,重力做的功为2mgh | |
| C. | 足球由2运动到3的过程中,重力势能减少了mgh | |
| D. | 足球由2运动到3的过程中,重力势能增加了mgh |
 如图所示,处于真空的点电荷a、b、c、d的电荷量分别为+q、+q、-q、-q,四边形abcd为菱形,∠a=60°.1、2、3、4分别为所在边的中点,其对应边的电场强度大小分别为E1、E2、E3、E4,对应的电势分别为φ1、φ2、φ3、φ4,则下列说法正确的是( )
如图所示,处于真空的点电荷a、b、c、d的电荷量分别为+q、+q、-q、-q,四边形abcd为菱形,∠a=60°.1、2、3、4分别为所在边的中点,其对应边的电场强度大小分别为E1、E2、E3、E4,对应的电势分别为φ1、φ2、φ3、φ4,则下列说法正确的是( )| A. | E1=E3、φ1=φ3 | B. | E2=E4、φ2=φ4 | C. | E1=E3、φ1>φ3 | D. | E2=E4、φ2>φ4 |
 如图所示,为某物体在0-t3时间内的速度--时间图象,其中t3-t2=t2-t1=$\frac{1}{2}$t1,v1=-3v2,则下列说法正确的是( )
如图所示,为某物体在0-t3时间内的速度--时间图象,其中t3-t2=t2-t1=$\frac{1}{2}$t1,v1=-3v2,则下列说法正确的是( )| A. | 0-t3时间内,速度方向改变了三次 | |
| B. | 0-t3时间内,加速度方向改变了两次 | |
| C. | 0-t1时间内,物体的位移为$\frac{1}{3}$v1t1 | |
| D. | t1-t2和t2-t3时间内时间内物体的位移大小之比小于3:1 |
| A. | 力的单位N | B. | 电流的单位A | C. | 功的单位J | D. | 电压的单位V |
| A. | 物体所受合力为零,机械能一定守恒 | |
| B. | 物体所受的合力不等于零,机械能可能守恒 | |
| C. | 物体做匀速直线运动,机械能一定守恒 | |
| D. | 物体所受合力做功为零,机械能一定守恒 |
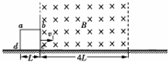 在光滑绝缘的水平地面上方,有一个宽度为4L、磁感应强度大小为B的匀强磁场区域,如图所示,一个边长为L、质量为m、电阻为R的金属正方形单匝线圈abcd在水平拉力作用下,沿垂直磁场方向,以初速度v1匀速进入磁场,当完全进入磁场后,撤去拉力,之后线圈ad边以速度v2离开磁场,线圈离开磁场所用的时间为t.
在光滑绝缘的水平地面上方,有一个宽度为4L、磁感应强度大小为B的匀强磁场区域,如图所示,一个边长为L、质量为m、电阻为R的金属正方形单匝线圈abcd在水平拉力作用下,沿垂直磁场方向,以初速度v1匀速进入磁场,当完全进入磁场后,撤去拉力,之后线圈ad边以速度v2离开磁场,线圈离开磁场所用的时间为t.