题目内容
如图所示,质量为0.4kg的木块以2m/s的速度水平地滑上静止的平板小车,车的质量为1.6kg,木块与小车之间的摩擦系数为0.2(g取10m/s2)。设小车足够长,求:
(1)木块和小车相对静止时小车的速度。
(2)从木块滑上小车到它们处于相对静止所经历的时间。
(3)从木块滑上小车到它们处于相对静止木块在小车上滑行的距离。

(1)0.4m/s
(2)0.8s
(3)0.8m
解析:
(1)以木块和小车为研究对象,系统所受合外力为零,系统动量守恒,以木块速度方向为正方向,由动量守恒定律可得:
木块m 小车M
初:v0=2m/s v0=0
末:v v
即mv0=(M+m)v,
得![]() 。
。
(2)再以木块为研究对象,其受力情况如图所示,由动量定理可得:


![]() 。
。
(3)木块做匀减速运动,加速度![]() ,
,
车做匀加速运动,加速度![]() ,由运动学公式可得:
,由运动学公式可得:
vt2-v02=2as,
在此过程中木块的位移![]() ,
,
车的位移![]() ,
,
由此可知,木块在小车上滑行的距离为ΔS=S1-S2=0.8m,即为所求。
另解:设小车的位移为S2,则A的位移为S1+ΔS,ΔS为木块在小车上滑行的距离,那么小车、木块之间的位移差就是ΔS,作出木块、小车的v-t图线如图所示,则木块在小车上的滑行距离数值上等于图中阴影部分的三角形的“面积”。


练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 如图所示,质量为0.5kg的物块以5m/s的初速度从斜面顶端下滑,斜面长5m,倾角为37°,物块与斜面间的动摩擦因数μ=0.5.求:
如图所示,质量为0.5kg的物块以5m/s的初速度从斜面顶端下滑,斜面长5m,倾角为37°,物块与斜面间的动摩擦因数μ=0.5.求: 如图所示,质量为0.1kg的小球从竖立的轻质弹簧正上端C(状态甲)由静止自由下落到弹簧上端B(状态乙),B为弹簧处于自然状态的位置,A为弹簧压缩到的最低位置(状态丙).已知A、B的高度差为0.3m,B、C的高度差为0.5m,g=10m/s2.则下列说法正确的是( )
如图所示,质量为0.1kg的小球从竖立的轻质弹簧正上端C(状态甲)由静止自由下落到弹簧上端B(状态乙),B为弹簧处于自然状态的位置,A为弹簧压缩到的最低位置(状态丙).已知A、B的高度差为0.3m,B、C的高度差为0.5m,g=10m/s2.则下列说法正确的是( ) 如图所示,质量为0.5kg的小球,从桌面以上高1.2m的A点下落到地面的B点,已知桌面高0.8m,求:
如图所示,质量为0.5kg的小球,从桌面以上高1.2m的A点下落到地面的B点,已知桌面高0.8m,求: 如图所示,质量为0.2kg的物体带正电,其电量为4×10-4C,从半径为0.3m光滑的
如图所示,质量为0.2kg的物体带正电,其电量为4×10-4C,从半径为0.3m光滑的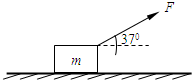 如图所示,质量为0.78kg的金属块放在水平桌面上,在与水平成37°角斜向上、大小为3.0N的拉力F作用下,以4.0m/s的速度向右做匀速直线运动.已知sin37°=0.60,cos37°=0.80,g取10m/s2.
如图所示,质量为0.78kg的金属块放在水平桌面上,在与水平成37°角斜向上、大小为3.0N的拉力F作用下,以4.0m/s的速度向右做匀速直线运动.已知sin37°=0.60,cos37°=0.80,g取10m/s2.