��Ŀ����
�ڹ⻬ˮƽ������һ������ڶ��⻬������ΪM�����ף���������һ����Ϊm�Ļ�������֪M��m�������ܷ�һ�����������壮�ֶ�����ʩ��һ��ˮƽ���������F����ͼ����ʾ��ʱ�����ļ��ٶ�Ϊa1����������ѹǿΪp1�����ΪV1������ͬ����С����Fˮƽ�����ƻ�������ͼ����ʾ������ʱ���ļ��ٶ�Ϊa2����������ѹǿΪp2�����ΪV2�����ܷ�������������¶Ⱦ����䣬��
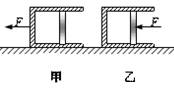
A��a1 = a2��p1��p2��V1��V2
B��a1��a2��p1��p2��V1��V2
C��a1 = a2��p1��p2��V1��V2
D��a1��a2��p1��p2��V1��V2
A
��������F = ma�ã�a1 = a2����Ϊp1 = p0��p2�� p0 ����p1 ��p2 ��V1��V2��
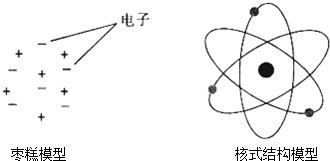
��ʾ�����Է���ѹǿ���¶ȡ����֮��Ĺ�ϵҪ�����������״̬�����������壬���У�����ѹǿ�Ǵ�������Ƶ����ײ�����γɵģ����뵥λ����ڵķ����������ӵ�ƽ�������йأ������ӵ�ƽ�����ܿ��ɺ�۵��¶���������
��������˵������������̬����![]()
![]() �⣬��Ӧע�����з�����·�����¶ȡ�����ƽ�����ܡ�����ƽ�����ʡ���ײ����ѹǿ��������������ܼ��ȡ�ѹǿ�����¶ȱ������ƽ�����ܱ���ܷ��Ӷ��ܱ����������ܱ䡣
�⣬��Ӧע�����з�����·�����¶ȡ�����ƽ�����ܡ�����ƽ�����ʡ���ײ����ѹǿ��������������ܼ��ȡ�ѹǿ�����¶ȱ������ƽ�����ܱ���ܷ��Ӷ��ܱ����������ܱ䡣

 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�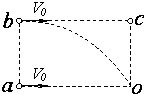 ��ͼ��ʾ���ڹ⻬ˮƽ������һ��С��a�Գ��ٶ�v0�˶���ͬʱ���������Ϸ���һС��bҲ��v0���ٶ�ˮƽ�׳���������O�㣬��O�����Ϸ�����b�ȸߴ���һС��cҲ��ͬһʱ�������������˶���������
��ͼ��ʾ���ڹ⻬ˮƽ������һ��С��a�Գ��ٶ�v0�˶���ͬʱ���������Ϸ���һС��bҲ��v0���ٶ�ˮƽ�׳���������O�㣬��O�����Ϸ�����b�ȸߴ���һС��cҲ��ͬһʱ�������������˶���������| A��С��a�ȵ���O�� | B��С��b�ȵ���O�� | C������ͬʱ����O�� | D��a��b��c�����ܷ�ͬʱ���ﲻ��ȷ�� |
 ��2008?������һģ���ڹ⻬ˮƽ������һ������ڶ��⻬������ΪM�����ף���������һ����Ϊm�Ļ�������֪M��m�������ܷ�һ�����������壮�ֶ�����ʩ��һ��ˮƽ���������F����ͼA��ʱ�����ļ��ٶ�Ϊa1����������ѹǿΪp1�����ΪV1������ͬ����С����Fˮƽ�����ƻ�������ͼB������ʱ���ļ��ٶ�Ϊa2����������ѹǿΪp2�����ΪV2�����ܷ�������������¶Ⱦ����䣬������
��2008?������һģ���ڹ⻬ˮƽ������һ������ڶ��⻬������ΪM�����ף���������һ����Ϊm�Ļ�������֪M��m�������ܷ�һ�����������壮�ֶ�����ʩ��һ��ˮƽ���������F����ͼA��ʱ�����ļ��ٶ�Ϊa1����������ѹǿΪp1�����ΪV1������ͬ����С����Fˮƽ�����ƻ�������ͼB������ʱ���ļ��ٶ�Ϊa2����������ѹǿΪp2�����ΪV2�����ܷ�������������¶Ⱦ����䣬������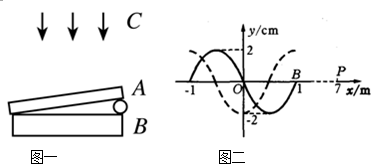
 �ڹ⻬ˮƽ������һ������ͬʱ�ܵ�����ˮƽ��F1��F2�����ã��ڵ�1s�ڱ��־�ֹ��������F1��F2��ʱ��ı仯��ͼ��ʾ��������˵����ȷ���ǣ�������
�ڹ⻬ˮƽ������һ������ͬʱ�ܵ�����ˮƽ��F1��F2�����ã��ڵ�1s�ڱ��־�ֹ��������F1��F2��ʱ��ı仯��ͼ��ʾ��������˵����ȷ���ǣ������� ��2006?��ƽ��ģ�⣩�ڹ⻬ˮƽ������һ������ͬʱ�ܵ�����ˮƽ��F1��F2�����ã��ڵ�1s�����屣�־�ֹ״̬��������F1��F2��ʱ��ı仯��ͼ��ʾ��������˵������ȷ���ǣ�������
��2006?��ƽ��ģ�⣩�ڹ⻬ˮƽ������һ������ͬʱ�ܵ�����ˮƽ��F1��F2�����ã��ڵ�1s�����屣�־�ֹ״̬��������F1��F2��ʱ��ı仯��ͼ��ʾ��������˵������ȷ���ǣ�������