��Ŀ����
����Ŀ����ͼ����ʾ,y���Ҳ�ռ��д�ֱxOyƽ��������ʱ��仯�Ĵų�,ͬʱ������y�Ḻ�������ǿ�糡(ͼ�е糡δ����),�Ÿ�Ӧǿ����ʱ��仯������ͼ����ʾ(ͼ��B0��֪,��������Ϊδ֪)��t=0ʱ��,һ����Ϊm�������Ϊ+q�Ĵ����������ٶ�v0������ԭ��O��x������������糡�ʹų�����,t0ʱ�����ӵ�������Ϊ(x0,y0)�ĵ�A(x0>y0),�ٶȴ�СΪv,������x��������,��ʱ��ȥ�糡,t2ʱ�����Ӿ���x����x=x0��,�ٶ���x��������,������������,��:
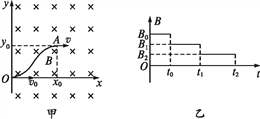
(1)0~t0ʱ����O��A�������Ʋ�UOA;
(2)������t=0ʱ�̵ļ��ٶȴ�Сa;
(3)B1����Сֵ��B2����Сֵ�ı���ʽ��
���𰸡�(1) ![]() (2)
(2) ![]() (3)
(3) ![]() ��
��![]()
��������
��1�����Ӵ�O��A�����ɶ��ܶ���������������ĵ�ѹ����2����ţ�ٵڶ����ɿ���������ӵļ��ٶȣ���3�����������˶��켣���ɼ���֪ʶ������ӵĹ���뾶�������ڴų���������Բ���˶����������ṩ��������Ӧ��ţ�ٵڶ����ɿ�������Ÿ�Ӧǿ�ȣ�
��1������������O��A�˶������У��ɶ��ܶ����ã�![]()
�����![]()
��2����糡ǿ�ȴ�СΪE����![]()
t=0ʱ�̣���ţ�ٵڶ����ɵ���![]()
�����![]()
��3��![]() ʱ���ڣ�������С������Բ���˶���
ʱ���ڣ�������С������Բ���˶���![]() ʱ�����Ӵ�C�������Բ����Բ���뾶Ϊ
ʱ�����Ӵ�C�������Բ����Բ���뾶Ϊ![]() ����ӦСԲ���뾶ΪR��
����ӦСԲ���뾶ΪR��
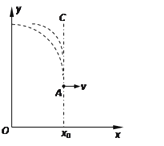
�ɼ��ι�ϵ�У�![]()
��![]()
![]() ����Сֵ
����Сֵ![]()
��Ӧ��![]() ȡ��Сֵ������������C�㵽����x����
ȡ��Сֵ������������C�㵽����x����![]() ���ʱ��
���ʱ��![]() ����
����![]() ��k=0��1��2������
��k=0��1��2������

 �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�