题目内容
某小组同学用如图1所示的DIS二维运动实验系统研究单摆在运动过程中机械能的转化和守恒(忽略空气阻力).实验时,使发射器(相当于摆球)偏离平衡位置后由静止释放,使其在竖直平面内摆动.系统每隔0.02s记录一次发射器的位置,多次往复运动后,在计算机屏幕上得到的发射器在竖直平面内的运动轨迹如图2所示.
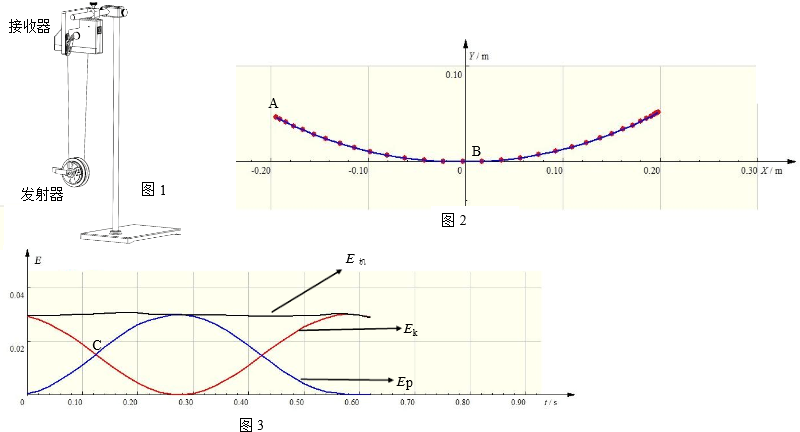
(1)图2中A点的速度 B点的速度.(填“大于”、“等于”或“小于”)
(2)在运动轨迹上选取适当区域后,点击“计算数据”,系统即可计算出摆球在所选区域内各点的重力势能、动能及总机械能,并绘出对应的图线,如图3所示.结合图2和图3综合分析,图3中t=0时刻对应图2中的 点(填“A”或“B”).由图3可知,此单摆的周期为 s.
(3)图3中的C点对应在图2中圆弧轨迹AB上的某一点,该点在
A.圆弧AB中点的左侧
B.圆弧AB中点的右侧
C.圆弧AB的中点
D.信息不够,不能确定.

(1)图2中A点的速度
(2)在运动轨迹上选取适当区域后,点击“计算数据”,系统即可计算出摆球在所选区域内各点的重力势能、动能及总机械能,并绘出对应的图线,如图3所示.结合图2和图3综合分析,图3中t=0时刻对应图2中的
(3)图3中的C点对应在图2中圆弧轨迹AB上的某一点,该点在
A.圆弧AB中点的左侧
B.圆弧AB中点的右侧
C.圆弧AB的中点
D.信息不够,不能确定.
分析:(1)根据动能定理,通过重力做功判断A、B两点的速度大小.
(2)根据t=0时刻对应的动能和重力势能确定对应的位置,抓住一个周期内,两次通过平衡位置,求出单摆的周期.
(3)C点动能和重力势能相等,根据机械能守恒定律确定出C点的高度与最大高度的关系,从而确定C点的位置.
(2)根据t=0时刻对应的动能和重力势能确定对应的位置,抓住一个周期内,两次通过平衡位置,求出单摆的周期.
(3)C点动能和重力势能相等,根据机械能守恒定律确定出C点的高度与最大高度的关系,从而确定C点的位置.
解答:解:(1)B到A,重力做负功,动能减小,则A点的速度小于B点的速度.
(2)t=0时刻,动能最大,重力势能最小,可知t=0时刻对应图2中的B点.从平衡位置出发,一个周期内,两次通过平衡位置,则T=0.56×2=1.12s.
(3)C点为重力势能和动能相等的点,根据机械能守恒定律得,
mv2=mgh′+
mv′2=2mgh′,解得h′=
,又
mv2=mgh,解得h=
,知重力势能与动能相等的位置的高度是最大高度的一半,可知C点处于圆弧AB中点的左侧.故A正确,B、C、D错误.
故选A.
故答案为:(1)小于 (2)B,1.12(1.0-1.2均可) (3)A
(2)t=0时刻,动能最大,重力势能最小,可知t=0时刻对应图2中的B点.从平衡位置出发,一个周期内,两次通过平衡位置,则T=0.56×2=1.12s.
(3)C点为重力势能和动能相等的点,根据机械能守恒定律得,
| 1 |
| 2 |
| 1 |
| 2 |
| v2 |
| 4g |
| 1 |
| 2 |
| v2 |
| 2g |
故选A.
故答案为:(1)小于 (2)B,1.12(1.0-1.2均可) (3)A
点评:解决本题的关键知道单摆在整个运动过程中动能、重力势能、机械能的变化,运用机械能守恒定律进行分析.

练习册系列答案
相关题目
(9分)在《探究加速度与力、质量的关系》实验中
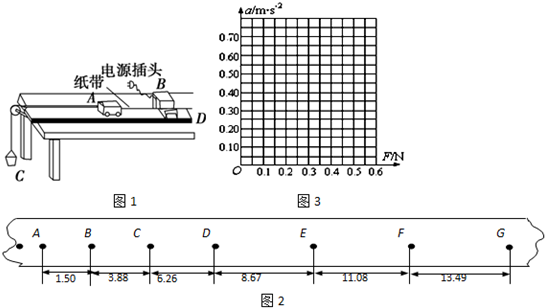
(1)某小组同学用如图所示装置,采用控制变量方法,来研究在小车质量不变的情况下,小车加速度与小车受力的关系。下列措施中正确的是( )
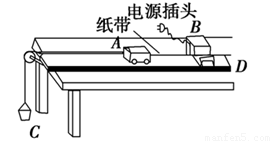
A.平衡摩擦力的方法就是将木板一端垫高,在塑料小桶中添加砝码,使小车在绳的拉力作用下能匀速滑动
B.每次改变小车所受的拉力时,不需要重新平衡摩擦力
C.实验中应先放小车,然后再开打点计时器的电源
D.在每次实验中,应使小车和砝码的质量远大于砂和小桶的总质量
(2)如图所示是某一次打点计时器打出的一条记录小车运动的纸带.取计数点A、B、C、D、E、F、G.纸带上两相邻计数点的时间间隔为T = 0.10s,用刻度尺测量出各相邻计数点间的距离分别为AB=1.50cm,BC=3.88 cm,CD=6.26 cm,DE=8.67 cm,EF=11.08 cm,FG=13.49cm,则小车运动的加速度大小a = _____ m/s2,打纸带上C点时小车的瞬时速度大小v C = ______ m/s.(结果保留二位有效数字)
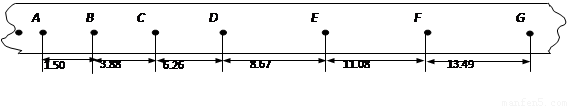
(3).某同学测得小车的加速度a和拉力F的数据如下表所示:(小车质量保持不变)
|
F/N |
0.20 |
0.30 |
0.40 |
0.50 |
0.60 |
|
a/ m/s2 |
0.30 |
0.40 |
0.48 |
0.60 |
0.72 |
①请根据表中的数据在坐标图上作出a—F图象
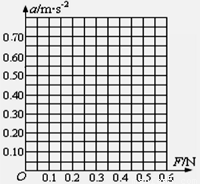
②图象不过坐标原点的原因可能是______________________________________。