题目内容
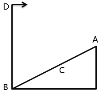
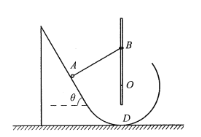
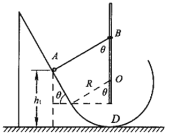
【题目】如图所示，光滑斜面倾角θ=60°，其底端与竖直平面内半径为R的光滑圆弧轨道平滑对接，位置D为圆弧轨道的最低点。两个质量均为m的小球A和小环B（均可视为质点）用L=1.5R的轻杆通过轻质铰链相连，B套在固定竖直光滑的长杆上，杆和圆轨道在同一竖直平面内，杆过轨道圆心，初始时轻杆与斜面垂直。在斜面上由静止释放A，假设在运动过程中两杆不会碰撞，小球通过轨道连接处时无能量损失（速度大小不变）。重力加速度为g。求：
(1)刚释放时，球A的加速度大小；
(2)小球A运动到最低点时的速度大小；
(3)已知小球以运动到最低点时，小环B的瞬时加速度大小为a，求此时小球A受到圆弧轨道的支持力大小。
【答案】(1)
；(2)
；(3)
【解析】
(1)由牛顿第二定律得
解得
(2)小球
初始位置距水平面高度设为
，由几何关系得
解得
小环
初始位置距水平面高度设为
，由几何关系得
解得
由系统机械能守恒
式中
，
，
解得
(3)以小环为研究对象，由牛顿第二定律得
以小球为研究对象，由牛顿第二定律得
解得
练习册系列答案
相关题目
