题目内容
（2009?安徽）如图所示，匀强电场方向沿x轴的正方向，场强为E．在A（d，0）点有一个静止的中性微粒，由于内部作用，某一时刻突然分裂成两个质量均为m的带电微粒，其中电荷量为q的微粒1沿y轴负方向运动，经过一段时间到达（0，-d）点．不计重力和分裂后两微粒间的作用．试求（1）分裂时两个微粒各自的速度；
（2）当微粒1到达（0，-d）点时，电场力对微粒1做功的瞬间功率；
（3）当微粒1到达（0，-d）点时，两微粒间的距离．
分析：（1）微粒1做的是类平抛运动，根据类平抛运动的规律可以求得微粒1的速度的大小，再由动量守恒求得微粒2的速度的大小；
（2）电场力做功的瞬时功率，要用沿电场力方向的瞬时速度的大小，再由P=Fv可以求得瞬时功率的大小；
（3）画出粒子的运动轨迹，由几何知识可以求得两微粒间的距离．
（2）电场力做功的瞬时功率，要用沿电场力方向的瞬时速度的大小，再由P=Fv可以求得瞬时功率的大小；
（3）画出粒子的运动轨迹，由几何知识可以求得两微粒间的距离．
解答：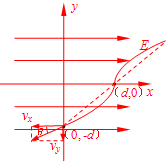
解：（1）微粒1在y方向不受力，做匀速直线运动；在x方向由于受恒定的电场力，做匀加速直线运动．所以微粒1做的是类平抛运动．
设微粒1分裂时的速度为v1，微粒2的速度为v2则有：
在y方向上有
d=v1t
在x方向上有a=
，
d=
at2
v1=
速度方向沿y轴的负方向．
中性微粒分裂成两微粒时，遵守动量守恒定律，有
mv1+mv2=0
所以 v2=-v1
所以 v2的大小为
，方向沿y正方向．
（2）设微粒1到达（0，-d）点时的速度为VB，则电场力做功的瞬时功率为，
P=qEVB cosθ=qEVBx，
其中由运动学公式 VBx=
=
，
所以 P=qE
，
（3）两微粒的运动具有对称性，如图所示，当微粒1到达（0，-d）点时发生的位移
S1=
d，
则当微粒1到达（0，-d）点时，两微粒间的距离为BC=2S1=2
d．
答：（1）分裂时微粒1的速度大小为
，方向沿着y轴的负方向；微粒2的速度大小为
，方向沿着y轴的正方向；
（2）当微粒1到达（0，-d）点时，电场力对微粒1做功的瞬间功率是 qE
；
（3）当微粒1到达（0，-d）点时，两微粒间的距离是2
d．
解：（1）微粒1在y方向不受力，做匀速直线运动；在x方向由于受恒定的电场力，做匀加速直线运动．所以微粒1做的是类平抛运动．设微粒1分裂时的速度为v1，微粒2的速度为v2则有：
在y方向上有
d=v1t
在x方向上有a=
| qE |
| m |
d=
| 1 |
| 2 |
v1=
|
速度方向沿y轴的负方向．
中性微粒分裂成两微粒时，遵守动量守恒定律，有
mv1+mv2=0
所以 v2=-v1
所以 v2的大小为
|
（2）设微粒1到达（0，-d）点时的速度为VB，则电场力做功的瞬时功率为，
P=qEVB cosθ=qEVBx，
其中由运动学公式 VBx=
| 2ad |
|
所以 P=qE
|
（3）两微粒的运动具有对称性，如图所示，当微粒1到达（0，-d）点时发生的位移
S1=
| 2 |
则当微粒1到达（0，-d）点时，两微粒间的距离为BC=2S1=2
| 2 |
答：（1）分裂时微粒1的速度大小为
|
|
（2）当微粒1到达（0，-d）点时，电场力对微粒1做功的瞬间功率是 qE
|
（3）当微粒1到达（0，-d）点时，两微粒间的距离是2
| 2 |
点评：带电微粒在电场中运动，一般不考虑重力的作用，只是受到电场力的作用，再进一步判断微粒的运动情况，本题中微粒做类平抛运动，由类平抛运动的规律就可以求得速度，在计算功率时一定要注意求的是瞬时功率，注意公式的选择．
练习册系列答案
相关题目
（2009?安徽模拟）如图所示，竖直放置在水平面上的轻质弹簧上叠放着两物块A、B，两者的质量均为2kg，它们处于静止状态．若突然将一个大小为10N、方向竖直向下的力施加在物体A上，则此瞬间A对B的压力大小为：（g=10m/s2）（ ）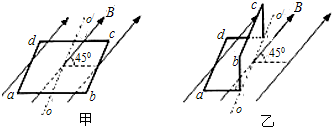
（2009?安徽）如图甲所示，一个电阻为R，面积为S的矩形导线框abcd，水平旋转在匀强磁场中，磁场的磁感应强度为B，方向与ad边垂直并与线框平面成45°角，o、o′分别是ab和cd边的中点．现将线框右半边obco′绕oo′逆时针90°到图乙所示位置．在这一过程中，导线中通过的电荷量是（ ）
（2009?安徽模拟）如图所示，甲、乙两物体分别固定在一根弹簧的两端，并放在光滑水平的桌面上，两物体的质量分别为m1和m2，弹簧的质量不能忽略．甲受到方向水平向左的拉力Fl作用，乙受到水平向右的拉力F2作用．下列说法正确的是（ ）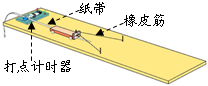
（2009?安徽）探究力对原来静止的物体做的功与物体获得的速度的关系，实验装置如图所示，实验主要过程如下：