题目内容
两个氘核发生了如下核反应 +
+ →
→ +
+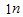 ,其中氘核的质量为2.0136u,氦核的质量为3.0150u,中子的质量为1.0087u.
,其中氘核的质量为2.0136u,氦核的质量为3.0150u,中子的质量为1.0087u.(1)若反应前两个氘核的动能都为0.35MeV,进行对心碰撞,并且结合能全部转化为机械能,求反应中产生的中子和氦核的动能.
(2)假设反应中产生的氦核沿直线向静止的碳核(
 )接近,受库仑力的影响,当它们距离最近时,两个原子核的动能各是多少?
)接近,受库仑力的影响,当它们距离最近时,两个原子核的动能各是多少?
【答案】分析:(1)根据质能方程求出反应释放的能量,由反应中能量守恒和动量守恒列出等式求解.
(2)氦核与静止的碳核对心正碰后,当它们相距最近时,两核的速度相等,相当于完全非弹性碰撞模型,由动量守恒定律列出等式求解.
解答:解:(1)反应中的质量亏损△m=2mD-mHe-mn=2×2.0136-(3.0150+1.0087)=0.0035u
所以释放的能量为△E=△mC2=0.0035×931.5MeV=3.26MeV
设反应中生成的中子和氦核的速率分别为v′1和v′2由反应中能量守恒和动量守恒有
0=mnv′1-mHev′2 ①
△E+2E= mn
mn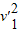 +
+ mHe
mHe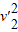 ②
②
其中E=0.35MeV
由①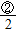 得到
得到
∴EkHe=0.99MeV,Ekn=2.97MeV
(2)氦核与静止的碳核对心正碰后,当它们相距最近时,两核的速度相等,相当于完全非弹性碰撞模型,
由动量守恒定律有 mHev′2=(mHe+mc)v′3
∴v′3=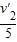 ,此时,氦核的动能E′kHe和碳核的动能E′kc分别为
,此时,氦核的动能E′kHe和碳核的动能E′kc分别为
E′kHe=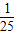 EkHe≈0.04MeV
EkHe≈0.04MeV
E′kc=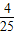 EkHe≈0.16MeV.
EkHe≈0.16MeV.
点评:对于核反应书写核反应方程,要抓住微观粒子的碰撞,相当于弹性碰撞,遵守两大守恒:动量守恒和能量守恒.
(2)氦核与静止的碳核对心正碰后,当它们相距最近时,两核的速度相等,相当于完全非弹性碰撞模型,由动量守恒定律列出等式求解.
解答:解:(1)反应中的质量亏损△m=2mD-mHe-mn=2×2.0136-(3.0150+1.0087)=0.0035u
所以释放的能量为△E=△mC2=0.0035×931.5MeV=3.26MeV
设反应中生成的中子和氦核的速率分别为v′1和v′2由反应中能量守恒和动量守恒有
0=mnv′1-mHev′2 ①
△E+2E=
 mn
mn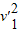 +
+ mHe
mHe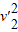 ②
②其中E=0.35MeV
由①
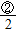 得到
得到∴EkHe=0.99MeV,Ekn=2.97MeV
(2)氦核与静止的碳核对心正碰后,当它们相距最近时,两核的速度相等,相当于完全非弹性碰撞模型,
由动量守恒定律有 mHev′2=(mHe+mc)v′3
∴v′3=
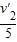 ,此时,氦核的动能E′kHe和碳核的动能E′kc分别为
,此时,氦核的动能E′kHe和碳核的动能E′kc分别为E′kHe=
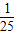 EkHe≈0.04MeV
EkHe≈0.04MeVE′kc=
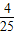 EkHe≈0.16MeV.
EkHe≈0.16MeV.点评:对于核反应书写核反应方程,要抓住微观粒子的碰撞,相当于弹性碰撞,遵守两大守恒:动量守恒和能量守恒.

练习册系列答案
相关题目
 ,其中氘核质量为2.1036u,氢核质量为3.1050u,中子质量为1.0087u。求:
,其中氘核质量为2.1036u,氢核质量为3.1050u,中子质量为1.0087u。求: C)接近,受库仑力的影响,当它们的距离最近时,两个原子核的动能各是多少?
C)接近,受库仑力的影响,当它们的距离最近时,两个原子核的动能各是多少?