题目内容
 如图所示,一根轻质细杆的两端分别固定着A、B两只质量均为m的小球,O点是一光滑水平轴,已知AO=a,BO=2a,使此装置在竖直平面内绕轴O转动,当A球转到最低点时速度为
如图所示,一根轻质细杆的两端分别固定着A、B两只质量均为m的小球,O点是一光滑水平轴,已知AO=a,BO=2a,使此装置在竖直平面内绕轴O转动,当A球转到最低点时速度为| ga |
2
| ga |
2
;此时轻质细杆对轴O的作用力大小为| ga |
mg
mg
,方向竖直向上
竖直向上
.分析:因A、B两球用轻杆相连,故两球转动的角速度相等,由v=rω,即可求出B球的速度.
小球A通过最低点时,受重力和杆的弹力作用,杆的弹力和重力和合力提供向心力,B球在最高点时,设杆对B球的弹力方向竖直向下.根据牛顿第二定律分别求出杆对两球的弹力大小,判断出方向,再求解轻质细杆对轴O的作用力大小和方向.
小球A通过最低点时,受重力和杆的弹力作用,杆的弹力和重力和合力提供向心力,B球在最高点时,设杆对B球的弹力方向竖直向下.根据牛顿第二定律分别求出杆对两球的弹力大小,判断出方向,再求解轻质细杆对轴O的作用力大小和方向.
解答:解:A、B两球转动的角速度相等,由v=rω得:
=
=
由题知,vA=
,解得:vB=2
;
在最低点,对A球:设杆对它的弹力向上,大小为N1.B球在最高点,设杆对B球的弹力大小为N2,方向竖直向下.
根据牛顿第二定律,得:
对A:mg-N1=m
对B:N2+mg=m
解得:N1=2mg,方向竖直向上.
N2=mg,方向竖直向下.
根据牛顿第三定律得知,A球对杆的作用力大小为N1′=N1=2mg,方向竖直向下;
B球对杆的作用力大小为N2′=N2=mg,方向竖直向上;
所以此时轻质细杆对轴O的作用力大小为:F=N1′-N2′=mg,方向竖直向上
故答案为:2
;mg;竖直向上.
| vA |
| vB |
| a |
| 2a |
| 1 |
| 2 |
由题知,vA=
| ga |
| ga |
在最低点,对A球:设杆对它的弹力向上,大小为N1.B球在最高点,设杆对B球的弹力大小为N2,方向竖直向下.
根据牛顿第二定律,得:
对A:mg-N1=m
| ||
| a |
对B:N2+mg=m
| ||
| 2a |
解得:N1=2mg,方向竖直向上.
N2=mg,方向竖直向下.
根据牛顿第三定律得知,A球对杆的作用力大小为N1′=N1=2mg,方向竖直向下;
B球对杆的作用力大小为N2′=N2=mg,方向竖直向上;
所以此时轻质细杆对轴O的作用力大小为:F=N1′-N2′=mg,方向竖直向上
故答案为:2
| ga |
点评:本题关键是A、B球机械能均不守恒,但A与B系统机械能守恒.对于两球的受力,应根据牛顿运动定律求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
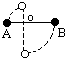 如图所示,一根轻质细杆的两端分别固定着A、B两只质量均为m的小球,O点是一光滑水平轴,已知AO=l,BO=2l,使细杆从水平位置由静止开始转动,当B球转到O点正下方时,它对细杆的拉力大小是多大?(提示:任一时刻两球的角速度相等).
如图所示,一根轻质细杆的两端分别固定着A、B两只质量均为m的小球,O点是一光滑水平轴,已知AO=l,BO=2l,使细杆从水平位置由静止开始转动,当B球转到O点正下方时,它对细杆的拉力大小是多大?(提示:任一时刻两球的角速度相等). ,
, 使细杆从水平位置由静止开始转动,当B球转到O点正下方时,求:(1)物体
使细杆从水平位置由静止开始转动,当B球转到O点正下方时,求:(1)物体 对细杆的拉力。(2)杆对B球做功
对细杆的拉力。(2)杆对B球做功 。
。
 ,
, 使细杆从水平位置由静止开始转动,当B球转到O点正下方时,求:(1)物体
使细杆从水平位置由静止开始转动,当B球转到O点正下方时,求:(1)物体 对细杆的拉力。(2)杆对B球做功
对细杆的拉力。(2)杆对B球做功 。
。
 ,若小球质量为m,则此时 ( )
,若小球质量为m,则此时 ( )