题目内容
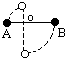 如图所示,一根轻质细杆的两端分别固定着A、B两只质量均为m的小球,O点是一光滑水平轴,已知AO=l,BO=2l,使细杆从水平位置由静止开始转动,当B球转到O点正下方时,它对细杆的拉力大小是多大?(提示:任一时刻两球的角速度相等).
如图所示,一根轻质细杆的两端分别固定着A、B两只质量均为m的小球,O点是一光滑水平轴,已知AO=l,BO=2l,使细杆从水平位置由静止开始转动,当B球转到O点正下方时,它对细杆的拉力大小是多大?(提示:任一时刻两球的角速度相等).分析:因A、B两球用轻杆相连,故两球转动的角速度相等,对A、B两球组成的系统应用机械能守恒定律并结合牛顿第二定律即可解题.
解答:解:对A、B两球组成的系统应用机械能守恒定律得:
mg2l-mgl=
mvA2+
mvB2…①
因A、B两球用轻杆相连,故两球转动的角速度相等,即:
=
…②
设B球运动到最低点时细杆对小球的拉力为T,由牛顿第二定律得:
T-mg=m
…③
解①②③得:T=1.8mg,
由牛顿第三定律知,B球对细杆的拉力大小等于1.8mg,方向竖直向下
答:它对细杆的拉力大小是1.8mg.
mg2l-mgl=
| 1 |
| 2 |
| 1 |
| 2 |
因A、B两球用轻杆相连,故两球转动的角速度相等,即:
| vA |
| l |
| vB |
| 2l |
设B球运动到最低点时细杆对小球的拉力为T,由牛顿第二定律得:
T-mg=m
| vB2 |
| 2l |
解①②③得:T=1.8mg,
由牛顿第三定律知,B球对细杆的拉力大小等于1.8mg,方向竖直向下
答:它对细杆的拉力大小是1.8mg.
点评:本题主要考查了机械能守恒定律及牛顿第二定律的直接应用,注意A、B两球用轻杆相连,两球转动的角速度相等.

练习册系列答案
相关题目
 如图所示,一根轻质细杆的两端分别固定着A、B两只质量均为m的小球,O点是一光滑水平轴,已知AO=a,BO=2a,使此装置在竖直平面内绕轴O转动,当A球转到最低点时速度为
如图所示,一根轻质细杆的两端分别固定着A、B两只质量均为m的小球,O点是一光滑水平轴,已知AO=a,BO=2a,使此装置在竖直平面内绕轴O转动,当A球转到最低点时速度为 ,
, 使细杆从水平位置由静止开始转动,当B球转到O点正下方时,求:(1)物体
使细杆从水平位置由静止开始转动,当B球转到O点正下方时,求:(1)物体 对细杆的拉力。(2)杆对B球做功
对细杆的拉力。(2)杆对B球做功 。
。
 ,
, 使细杆从水平位置由静止开始转动,当B球转到O点正下方时,求:(1)物体
使细杆从水平位置由静止开始转动,当B球转到O点正下方时,求:(1)物体 对细杆的拉力。(2)杆对B球做功
对细杆的拉力。(2)杆对B球做功 。
。
 ,若小球质量为m,则此时 ( )
,若小球质量为m,则此时 ( )