题目内容
【题目】宽9m的成型玻璃以2m/s的速度连续不断地向前行进，在切割工序处，金刚割刀的速度为10m/s，为了使割下的玻璃板都成规定尺寸的矩形，则：
（1）金刚割刀的速度方向与玻璃板的速度方向夹角的余弦值为多少？
（2）切割一次的时间多长？
（3）所生产的玻璃板的规格是怎样的？
【答案】
（1）
解：由题目条件知，割刀运动的速度是实际的速度，所以为合速度．其分速度的效果恰好相对玻璃垂直切割．
设割刀的速度v2的方向与玻璃板速度v1的方向之间的夹角为θ，要保证割下均是矩形的玻璃板，则由v2是合速度得
v1=v2 cos θ
所以cosθ= 
= 
，即有：θ=arccos
要割下矩形板，割刀速度方向与玻璃板速度成θ=arccos
（2）
解：切割一次的时间
t= 
= 
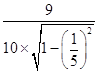≈0.92s
（3）
解：切割出的矩形玻璃板的规格为：
长度d=9 m，
宽度：l=v1t=2×0.92 m=1.84 m
【解析】为了使割下的玻璃板都成规定尺寸的矩形，知合速度的方向与玻璃板垂直，根据平行四边形定则求出金刚钻割刀的轨道方向，通过合速度求出切割一次的时间．根据等时性求出切割成的玻璃板长度．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
