题目内容
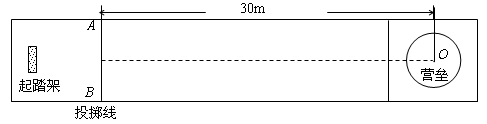
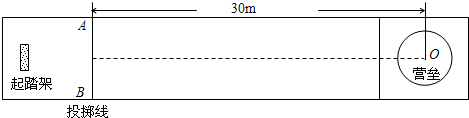
在2010年2月举行的温哥华冬奥会冰壶比赛中,我国女子冰壶队获得铜牌,显示了强大的实力.比赛场地示意如图,投掷线和营垒圆心相距s=30m,营垒半径R=1.8m,冰壶石质量均为19kg,可视为质点.某局比赛中,甲方运动员从起踏架处推着冰壶石C出发,在投掷线AB处放手让冰壶石以速度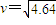 m/s沿虚线向圆心O点滑出.为保证比赛胜利,使冰壶石C能滑到圆心O点,将对方已停在O点的冰壶石D碰走,同时保证甲方冰壶石C能留在营垒内,且离圆心越近越好.按比赛规则,甲方运动员可在场地内任意位置刷冰,减小动摩擦因数,使冰壶石C以适当的速度碰走冰壶石D,乙方运动员可在两冰壶石相碰后越过D点时刷冰,减小动摩擦因数使冰壶石C滑出营垒.已知冰壶石与冰面间动摩擦因数μ1=0.008,甲方运动员通过刷冰可使动摩擦因数μ2减小到0.002,乙方运动员通过刷冰可使动摩擦因数μ3减小到0.0025.两冰壶石发生正碰,碰撞过程中系统能量损失为冰壶石C碰撞前动能的
m/s沿虚线向圆心O点滑出.为保证比赛胜利,使冰壶石C能滑到圆心O点,将对方已停在O点的冰壶石D碰走,同时保证甲方冰壶石C能留在营垒内,且离圆心越近越好.按比赛规则,甲方运动员可在场地内任意位置刷冰,减小动摩擦因数,使冰壶石C以适当的速度碰走冰壶石D,乙方运动员可在两冰壶石相碰后越过D点时刷冰,减小动摩擦因数使冰壶石C滑出营垒.已知冰壶石与冰面间动摩擦因数μ1=0.008,甲方运动员通过刷冰可使动摩擦因数μ2减小到0.002,乙方运动员通过刷冰可使动摩擦因数μ3减小到0.0025.两冰壶石发生正碰,碰撞过程中系统能量损失为冰壶石C碰撞前动能的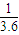 ,碰撞前后两冰壶石始终在同一直线上运动,g取10m/s2.比赛中两方依次投冰壶石,每队有4个人,每个人2个冰壶石.等到双方将冰壶石全部投完之后,一局便结束了,此时开始计算得分.求:
,碰撞前后两冰壶石始终在同一直线上运动,g取10m/s2.比赛中两方依次投冰壶石,每队有4个人,每个人2个冰壶石.等到双方将冰壶石全部投完之后,一局便结束了,此时开始计算得分.求: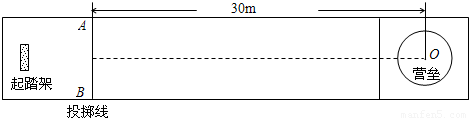
(1)若甲方运动员不刷冰,冰壶石C能滑行的最大距离是多少.
(2)为保证甲方在本局比赛中获胜,即冰壶石C不脱离营垒,冰壶石C碰撞前瞬间速度的大小;
(3)为保证甲方在本局比赛中获胜,即冰壶石C不脱离营垒,甲方运动员在投掷线AB到营垒圆心之间刷冰的最大距离是多少.
【答案】分析:(1)若甲方运动员不刷冰,根据动能定理研究冰壶石C能滑行的最大距离.
(2)为保证甲方在本局比赛中获胜,考虑对方运动员刷冰,冰壶C不脱离营垒时,根据动能定理求得碰撞后冰壶C的速度.冰壶石C、D碰撞过程遵守动量守恒,结合题中能量关系,列式可求出冰壶石C碰撞前瞬间速度的大小;
(3)为保证甲方在本局比赛中获胜,冰壶石C不脱离营垒,速度必须达到(2)中碰撞前瞬间的速度,根据动能定理求解甲方运动员在投掷线AB到营垒圆心之间刷冰的最大距离.
解答:解:(1)若甲方运动员不刷冰,设冰壶石滑行最大距离为s1,由动能定理得
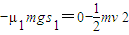
∴s1=29m
(2)设两冰壶石碰撞后,冰壶石C、D的速度分别是为v1、v2,考虑对方运动员刷冰,冰壶C不脱离营垒时,由动能定理得
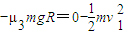
解得:v1=0.3m/s
两冰壶石相碰前,设冰壶石C的速度为v1′
由动量守恒定律得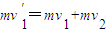
由能量守恒定律得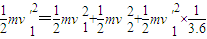
解得:v2=1.5m/s
∴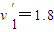 m/s
m/s
(3)设甲方运动员在冰壶石碰撞前刷冰的最大距离为s2
由动能定理得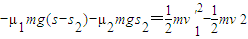
解得s2≈28.3m
答:(1)若甲方运动员不刷冰,冰壶石C能滑行的最大距离是29m.
(2)为保证甲方在本局比赛中获胜,即冰壶石C不脱离营垒,冰壶石C碰撞前瞬间速度的大小是1.8m/s;
(3)为保证甲方在本局比赛中获胜,即冰壶石C不脱离营垒,甲方运动员在投掷线AB到营垒圆心之间刷冰的最大距离是28.3m.
点评:本题整合了动能定理、动量守恒定律、能量守恒定律等多个规律,只要细心,可以正确解答
(2)为保证甲方在本局比赛中获胜,考虑对方运动员刷冰,冰壶C不脱离营垒时,根据动能定理求得碰撞后冰壶C的速度.冰壶石C、D碰撞过程遵守动量守恒,结合题中能量关系,列式可求出冰壶石C碰撞前瞬间速度的大小;
(3)为保证甲方在本局比赛中获胜,冰壶石C不脱离营垒,速度必须达到(2)中碰撞前瞬间的速度,根据动能定理求解甲方运动员在投掷线AB到营垒圆心之间刷冰的最大距离.
解答:解:(1)若甲方运动员不刷冰,设冰壶石滑行最大距离为s1,由动能定理得
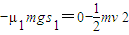
∴s1=29m
(2)设两冰壶石碰撞后,冰壶石C、D的速度分别是为v1、v2,考虑对方运动员刷冰,冰壶C不脱离营垒时,由动能定理得
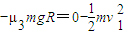
解得:v1=0.3m/s
两冰壶石相碰前,设冰壶石C的速度为v1′
由动量守恒定律得
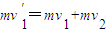
由能量守恒定律得
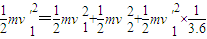
解得:v2=1.5m/s
∴
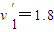 m/s
m/s(3)设甲方运动员在冰壶石碰撞前刷冰的最大距离为s2
由动能定理得
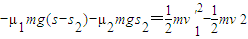
解得s2≈28.3m
答:(1)若甲方运动员不刷冰,冰壶石C能滑行的最大距离是29m.
(2)为保证甲方在本局比赛中获胜,即冰壶石C不脱离营垒,冰壶石C碰撞前瞬间速度的大小是1.8m/s;
(3)为保证甲方在本局比赛中获胜,即冰壶石C不脱离营垒,甲方运动员在投掷线AB到营垒圆心之间刷冰的最大距离是28.3m.
点评:本题整合了动能定理、动量守恒定律、能量守恒定律等多个规律,只要细心,可以正确解答

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目

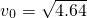 m/s沿虚线向圆心O点滑出.为保证比赛胜利,使冰壶石C能滑到圆心O点,将对方已停在O点的冰壶石D碰走,同时保证甲方冰壶石C能留在营垒内,且离圆心越近越好.按比赛规则,甲方运动员可在场地内任意位置刷冰,减小动摩擦因数,使冰壶石C以适当的速度碰走冰壶石D,乙方运动员可在两冰壶石相碰后越过D点时刷冰,减小动摩擦因数使冰壶石C滑出营垒.已知冰壶石与冰面间动摩擦因数μ1=0.008,甲方运动员通过刷冰可使动摩擦因数μ2减小到0.002,乙方运动员通过刷冰可使动摩擦因数μ3减小到0.0025.两冰壶石发生正碰,碰撞过程中系统能量损失为冰壶石C碰撞前动能的
m/s沿虚线向圆心O点滑出.为保证比赛胜利,使冰壶石C能滑到圆心O点,将对方已停在O点的冰壶石D碰走,同时保证甲方冰壶石C能留在营垒内,且离圆心越近越好.按比赛规则,甲方运动员可在场地内任意位置刷冰,减小动摩擦因数,使冰壶石C以适当的速度碰走冰壶石D,乙方运动员可在两冰壶石相碰后越过D点时刷冰,减小动摩擦因数使冰壶石C滑出营垒.已知冰壶石与冰面间动摩擦因数μ1=0.008,甲方运动员通过刷冰可使动摩擦因数μ2减小到0.002,乙方运动员通过刷冰可使动摩擦因数μ3减小到0.0025.两冰壶石发生正碰,碰撞过程中系统能量损失为冰壶石C碰撞前动能的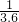 ,碰撞前后两冰壶石始终在同一直线上运动,g取10m/s2.比赛中两方依次投冰壶石,每队有4个人,每个人2个冰壶石.等到双方将冰壶石全部投完之后,一局便结束了,此时开始计算得分.求:
,碰撞前后两冰壶石始终在同一直线上运动,g取10m/s2.比赛中两方依次投冰壶石,每队有4个人,每个人2个冰壶石.等到双方将冰壶石全部投完之后,一局便结束了,此时开始计算得分.求: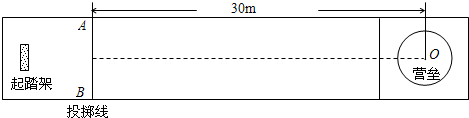
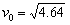 m/s沿虚线向圆心O点滑出。为保证比赛胜利,使冰壶石C能滑到圆心O点,将对方已停在O点的冰壶石D碰走,同时保证甲方冰壶石C能留在营垒内,且离圆心越近越好。按比赛规则,甲方运动员可在场地内任意位置刷冰,减小动摩擦因数,使冰壶石C以适当的速度碰走冰壶石D,乙方运动员可在两冰壶石相碰后越过D点时刷冰,减小动摩擦因数使冰壶石C滑出营垒。已知冰壶石与冰面间动摩擦因数
m/s沿虚线向圆心O点滑出。为保证比赛胜利,使冰壶石C能滑到圆心O点,将对方已停在O点的冰壶石D碰走,同时保证甲方冰壶石C能留在营垒内,且离圆心越近越好。按比赛规则,甲方运动员可在场地内任意位置刷冰,减小动摩擦因数,使冰壶石C以适当的速度碰走冰壶石D,乙方运动员可在两冰壶石相碰后越过D点时刷冰,减小动摩擦因数使冰壶石C滑出营垒。已知冰壶石与冰面间动摩擦因数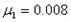 ,甲方运动员通过刷冰可使动摩擦因数
,甲方运动员通过刷冰可使动摩擦因数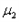 减小到0.002,乙方运动员通过刷冰可使动摩擦因数
减小到0.002,乙方运动员通过刷冰可使动摩擦因数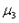 减小到0.0025。两冰壶石发生正碰,碰撞过程中系统能量损失为冰壶石C碰撞前动能的
减小到0.0025。两冰壶石发生正碰,碰撞过程中系统能量损失为冰壶石C碰撞前动能的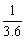 ,碰撞前后两冰壶石始终在同一直线上运动,g取10m/s2。比赛中两方依次投冰壶石,每队有4个人,每个人2个冰壶石。等到双方将冰壶石全部投完之后,一局便结束了,此时开始计算得分。求:
,碰撞前后两冰壶石始终在同一直线上运动,g取10m/s2。比赛中两方依次投冰壶石,每队有4个人,每个人2个冰壶石。等到双方将冰壶石全部投完之后,一局便结束了,此时开始计算得分。求: