题目内容
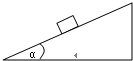 (2006?东城区一模)质量为m的小物块放在倾角为α的斜面上处于静止,如图所示.若整个装置可以沿水平方向或竖直方向平行移动,且小物块与斜面体总保持相对静止.下列的哪种运动方式可以使物块对斜面的压力和摩擦力都一定减小( )
(2006?东城区一模)质量为m的小物块放在倾角为α的斜面上处于静止,如图所示.若整个装置可以沿水平方向或竖直方向平行移动,且小物块与斜面体总保持相对静止.下列的哪种运动方式可以使物块对斜面的压力和摩擦力都一定减小( )分析:分析物体的受力情况,根据牛顿第二定律列式,分析物块所受的斜面的支持力和静摩擦力的变化,即可得解.
解答:解:A、设向上的加速度大小为a.物块受到重力mg、斜面的支持力N和摩擦力f三个力作用,物块的加速度方向竖直向上,根据牛顿第二定律可知物体所受的合外力方向竖直向上,而重力竖直向下,则知N和f的合力方向必定竖直向上,如图1所示,根据牛顿第二定律得
-mg=ma
f=Ntanα
解得,N=m(g+a)cosα,f=m(g+a)sinα
物块原来处于静止状态,a=0,N=mgcosα,f=mgsinα
可见,物块沿竖直方向向上加速运动时,所受的支持力和摩擦力都增大,则物块对斜面的压力和摩擦力都一定增大.故A错误.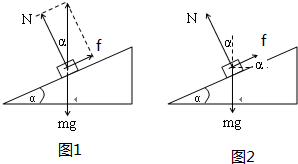
B、与A同理可得,物块沿竖直方向向上减速运动时,所受的支持力和摩擦力都减小,则物块对斜面的压力和摩擦力都一定减小.故B正确.
C、物块沿水平方向向右加速运动时,受力如图2所示,根据牛顿第二定律得:
fcosα-Nsinα=ma
fsinα-Ncosα=0
解得,N=mgcosθ-masinθ,f=mgsinθ+macosθ
可见,N减小,f增大,故C错误.
D、与C同理可知,物块沿水平方向向右减速运动时,当加速度a增大时,N增大,而f可能减小,也可能先减小到零后反向增大.故D错误.
故选B
| N |
| cosα |
f=Ntanα
解得,N=m(g+a)cosα,f=m(g+a)sinα
物块原来处于静止状态,a=0,N=mgcosα,f=mgsinα
可见,物块沿竖直方向向上加速运动时,所受的支持力和摩擦力都增大,则物块对斜面的压力和摩擦力都一定增大.故A错误.

B、与A同理可得,物块沿竖直方向向上减速运动时,所受的支持力和摩擦力都减小,则物块对斜面的压力和摩擦力都一定减小.故B正确.
C、物块沿水平方向向右加速运动时,受力如图2所示,根据牛顿第二定律得:
fcosα-Nsinα=ma
fsinα-Ncosα=0
解得,N=mgcosθ-masinθ,f=mgsinθ+macosθ
可见,N减小,f增大,故C错误.
D、与C同理可知,物块沿水平方向向右减速运动时,当加速度a增大时,N增大,而f可能减小,也可能先减小到零后反向增大.故D错误.
故选B
点评:分析受力情况,根据牛顿第二定律得到两个力的表达式,再进行分析,是常用的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
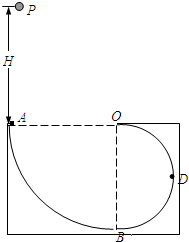 (2006?东城区一模)如图所示,ABDO是处于竖直平面内的光滑轨道,AB是半径为R=15m的
(2006?东城区一模)如图所示,ABDO是处于竖直平面内的光滑轨道,AB是半径为R=15m的 (2006?东城区一模)如图所示电路,闭合开关K,电动机M转动起来后,将滑动变阻器的滑动触头向左移动时,电动机中产生的电热功率Q随电压表测得的电压U和电流表测得的电流I而变化的情况是(电动机线圈的电阻可以认为是不变的)( )
(2006?东城区一模)如图所示电路,闭合开关K,电动机M转动起来后,将滑动变阻器的滑动触头向左移动时,电动机中产生的电热功率Q随电压表测得的电压U和电流表测得的电流I而变化的情况是(电动机线圈的电阻可以认为是不变的)( )