题目内容
9. 如图所示,发射远程轨道导弹,弹头脱离运载火箭后,在地球引力作用下,沿椭圆轨道飞行,击中地面目标B.C为椭圆的远地点,距地面高度为h.已知地球半径为R,地球质量为M,引力常量为G.关于弹头在C点的速度v和加速度a,正确的是( )
如图所示,发射远程轨道导弹,弹头脱离运载火箭后,在地球引力作用下,沿椭圆轨道飞行,击中地面目标B.C为椭圆的远地点,距地面高度为h.已知地球半径为R,地球质量为M,引力常量为G.关于弹头在C点的速度v和加速度a,正确的是( )| A. | v=$\sqrt{\frac{GM}{R+h}}$ a=$\frac{GM}{(R+h)^{2}}$ | B. | v<$\sqrt{\frac{GM}{R+h}}$ a=$\frac{GM}{(R+h)^{2}}$ | ||
| C. | v=$\sqrt{\frac{GM}{R+h}}$ a>$\frac{GM}{(R+h)^{2}}$ | D. | v<$\sqrt{\frac{GM}{R+h}}$ a<$\frac{GM}{(R+h)^{2}}$ |
分析 距地面高度为h的圆轨道上卫星的速度,根据牛顿第二定律得到其运动速度为$v=\sqrt{\frac{GM}{R+h}}$.C为轨道的远地点,导弹在C点的速度小于$\sqrt{\frac{GM}{R+h}}$.由牛顿第二定律求解导弹在C点的加速度.
解答 解:设距地面高度为h的圆轨道上卫星的速度为v,则由牛顿第二定律得:$G\frac{Mm}{(R+h)^{2}}=m\frac{{v}^{2}}{R+h}$,得到
$v=\sqrt{\frac{GM}{R+h}}$.导弹在C点只有加速才能进入卫星的轨道,所以导弹在C点的速度小于$\sqrt{\frac{GM}{R+h}}$.
由牛顿第二定律得:$G\frac{Mm}{(R+h)^{2}}=ma$,得导弹在C点的加速度为$a=\frac{GM}{(R+h)^{2}}$.
即v<$\sqrt{\frac{GM}{R+h}}$,$a=\frac{GM}{(R+h)^{2}}$.故B正确,ACD错误.
故选:B.
点评 本题运用牛顿第二定律、万有引力定律分析导弹与卫星运动问题.比较C在点的速度大小,可以结合卫星变轨知识来理解.

练习册系列答案
相关题目
14.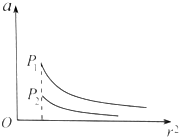 P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动,图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同,则( )
P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动,图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同,则( )
 P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动,图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同,则( )
P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s1、s2做匀速圆周运动,图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同,则( )| A. | P1的平均密度比P2的大 | B. | P1的第一宇宙速度比P2的小 | ||
| C. | s1的公转周期比s2的大 | D. | s1的向心加速度比s2的大 |
18.某实验小组利用拉力传感器和速度传感器探究“动能定理”.如图1所示,他们将拉力传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮与钩码相连,用拉力传感器记录小车受到拉力的大小.在水平桌面上相距50.0cm的A、B两点各安装一个速度传感器,记录小车通过A、B点时的速度大小,小车中可以放置砝码.
(1)实验主要步骤如下:
①测量小车和拉力传感器的总质量M1;把细线的一端固定在拉力传感器上,另一端通过定滑轮与钩码相连;正确连接所需电路.
②将小车由C点释放,小车在细线拉动下运动,记录细线拉力及小车通过A、B点时的速度.
③在小车中增加或减少砝码,重复②的操作.
在以上实验中,遗漏了平衡小车所受的摩擦力步骤.
(2)下列表格是他们用正确方法测得的一组数据,其中M是M1与小车中砝码质量M2之和,|v22-v12|是两个速度传感器记录速度的平方差,可以据此计算出动能变化量△E,F是拉力传感器测得的拉力,W是F在A、B间所做的功.表格中的△E3=0.600J,W3=0.610J.(结果保留三位有效数字)
数据记录表
(3)根据表格,请在图2中的方格纸上作出△E-W图线.
(4)根据△E-W图线,可得在实验误差允许的范围内,合外力所做的功等于物体动能的增量结论.

(1)实验主要步骤如下:
①测量小车和拉力传感器的总质量M1;把细线的一端固定在拉力传感器上,另一端通过定滑轮与钩码相连;正确连接所需电路.
②将小车由C点释放,小车在细线拉动下运动,记录细线拉力及小车通过A、B点时的速度.
③在小车中增加或减少砝码,重复②的操作.
在以上实验中,遗漏了平衡小车所受的摩擦力步骤.
(2)下列表格是他们用正确方法测得的一组数据,其中M是M1与小车中砝码质量M2之和,|v22-v12|是两个速度传感器记录速度的平方差,可以据此计算出动能变化量△E,F是拉力传感器测得的拉力,W是F在A、B间所做的功.表格中的△E3=0.600J,W3=0.610J.(结果保留三位有效数字)
数据记录表
| 次数 | M/kg | $\frac{({{v}_{2}}^{2}-{{v}_{1}}^{2})}{({m}^{2}•{s}^{-2})}$ | △E/J | F/N | W/J |
| 1 | 0.500 | 0.76 | 0.190 | 0.400 | 0.200 |
| 2 | 0.500 | 1.65 | 0.413 | 0.840 | 0.420 |
| 3 | 0.500 | 2.40 | △E3 | 1.220 | W3 |
| 4 | 1.000 | 2.40 | 1.200 | 2.420 | 1.210 |
| 5 | 1.000 | 2.84 | 1.420 | 2.860 | 1.430 |
(4)根据△E-W图线,可得在实验误差允许的范围内,合外力所做的功等于物体动能的增量结论.

16. 如图所示的电路中,U=180V,滑动变阻器R2的最大值为 200Ω,R1=100Ω.当滑片P滑至R2的中点时,a、b两端的电压为( )
如图所示的电路中,U=180V,滑动变阻器R2的最大值为 200Ω,R1=100Ω.当滑片P滑至R2的中点时,a、b两端的电压为( )
 如图所示的电路中,U=180V,滑动变阻器R2的最大值为 200Ω,R1=100Ω.当滑片P滑至R2的中点时,a、b两端的电压为( )
如图所示的电路中,U=180V,滑动变阻器R2的最大值为 200Ω,R1=100Ω.当滑片P滑至R2的中点时,a、b两端的电压为( )| A. | 40 V | B. | 60 V | C. | 80 V | D. | 120 V |

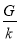 B.
B.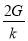 C.
C. D.
D.


 如图所示,在水平地面上并排放着高度相同,长度分别为LA=8.1cm,LB=12cm的两个木板A、B,他们的质量均为m0=10kg,且木板A、B与水平地面间的动摩擦因数均为μ0=0.2.某一时刻,一质量m=10kg的物块C(可视为质点)以一定速度滑上木板A的左端.已知物块C与两木板间的动摩擦因数μ=0.5,物块C恰好能滑到木板B的最右端,最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2.求:
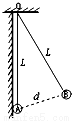
如图所示,在水平地面上并排放着高度相同,长度分别为LA=8.1cm,LB=12cm的两个木板A、B,他们的质量均为m0=10kg,且木板A、B与水平地面间的动摩擦因数均为μ0=0.2.某一时刻,一质量m=10kg的物块C(可视为质点)以一定速度滑上木板A的左端.已知物块C与两木板间的动摩擦因数μ=0.5,物块C恰好能滑到木板B的最右端,最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2.求: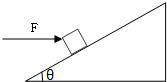 如图所示,质量为m的物体,放在一固定斜面上,物体与斜面间的动摩擦因数μ=$\frac{{\sqrt{3}}}{3}$当斜面倾角为θ时物体恰能沿斜面匀速下滑,此时再对物体施加一个大小为F的水平向右的恒力,物体可沿斜面匀速向上滑行.试求:
如图所示,质量为m的物体,放在一固定斜面上,物体与斜面间的动摩擦因数μ=$\frac{{\sqrt{3}}}{3}$当斜面倾角为θ时物体恰能沿斜面匀速下滑,此时再对物体施加一个大小为F的水平向右的恒力,物体可沿斜面匀速向上滑行.试求: