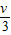��Ŀ����
������ΪM��ľ��̶��ڹ⻬ˮƽ���ϣ�һ������Ϊm���ӵ����ٶȦ�0��ˮƽ��������ľ�飬�ӵ��䴩ľ��ʱ���ٶ�Ϊ
���ֽ�ͬ����ľ����ڹ⻬��ˮƽ�����ϣ���ͬ���ӵ������ٶȦ�0��ˮƽ��������ľ�飬������˵����ȷ���ǣ�������
| v0 |
| 3 |
������ľ��̶�ʱ���ӵ��䴩ľ�飬�˷�Ħ�������Ĺ����ڲ��������ܣ����������غ���ʽ��ľ�鲻�̶�ʱ���ӵ�����ľ�飬ϵͳ�����غ㣬���費�ܴ�����������й�ͬ�ٶȣ����ݶ����غ㶨��������ͬ�ٶȺ��ݹ��ܹ�ϵ��ʽ����ӵ�������ȣ���������Ƿ�ì�ܣ��Ӷ��ж��Ƿ������
����⣺A��B��C��ľ��̶�ʱ���ӵ��䴩ľ�飬��ľ�鳤��Ϊd�����ݹ��ܹ�ϵ����
fd=
m
-
m��
��2
Q=
m
-
m��
��2
��
fd=Q=
m
��
f=
��
ľ�鲻�̶�ʱ���ӵ�����ľ�飬ϵͳ�����غ㣬���費�ܴ�����
���ݶ����غ㶨�ɣ���
mv0=��M+m��v
���ݹ��ܹ�ϵ����
Q��=fx=
m
-
��M+m��v2
�����⣬�У�M=3m
���
x=
��
����ʽ�����ʽ���õ�
x=
d��d
�ʼ���������ӵ������������A����B��ȷ��C����
D����ǰ�����֪����Ϊ��֪��M��m��ϵ������ȷ���ӵ��ܷ��ľ�飮��D����
��ѡB��
fd=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v0 |
| 3 |
Q=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v0 |
| 3 |
��
fd=Q=
| 4 |
| 9 |
| v | 2 0 |
��
f=
4m
| ||
| 9d |
ľ�鲻�̶�ʱ���ӵ�����ľ�飬ϵͳ�����غ㣬���費�ܴ�����
���ݶ����غ㶨�ɣ���
mv0=��M+m��v
���ݹ��ܹ�ϵ����
Q��=fx=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
�����⣬�У�M=3m
���
x=
3m
| ||
| 8f |
����ʽ�����ʽ���õ�
x=
| 27 |
| 32 |
�ʼ���������ӵ������������A����B��ȷ��C����
D����ǰ�����֪����Ϊ��֪��M��m��ϵ������ȷ���ӵ��ܷ��ľ�飮��D����
��ѡB��
����������ؼ��Ƕ��ӵ��䴩ľ��������ö����غ���ܹ�ϵ����������⣬Ȼ��Խ���������ۣ�

��ϰ��ϵ�д�
�����Ŀ
 ���ֽ�ͬ����ľ����ڹ⻬��ˮƽ�����ϣ���ͬ���ӵ������ٶȦ���ˮƽ��������ľ�飬������˵����ȷ���ǣ� ��
���ֽ�ͬ����ľ����ڹ⻬��ˮƽ�����ϣ���ͬ���ӵ������ٶȦ���ˮƽ��������ľ�飬������˵����ȷ���ǣ� ��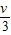 ���ֽ�ͬ����ľ����ڹ⻬��ˮƽ�����ϣ���ͬ���ӵ������ٶ�v��ˮƽ��������ľ�飬���ӵ���ľ���������������䣬������˵����ȷ���ǣ� ��
���ֽ�ͬ����ľ����ڹ⻬��ˮƽ�����ϣ���ͬ���ӵ������ٶ�v��ˮƽ��������ľ�飬���ӵ���ľ���������������䣬������˵����ȷ���ǣ� ��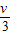 ���ֽ�ͬ����ľ����ڹ⻬��ˮƽ�����ϣ���ͬ���ӵ������ٶ�v��ˮƽ��������ľ�飮��֪ľ����ӵ�������С�㶨����M=3m�����ӵ��� ��
���ֽ�ͬ����ľ����ڹ⻬��ˮƽ�����ϣ���ͬ���ӵ������ٶ�v��ˮƽ��������ľ�飮��֪ľ����ӵ�������С�㶨����M=3m�����ӵ��� ��