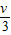题目内容
将质量为M的木块固定在光滑水平面上,一颗质量为m的子弹以速度υ沿水平方向射入木块,子弹射穿木块时的速度为 ,现将同样的木块放在光滑的水平桌面上,相同的子弹仍以速度υ沿水平方向射入木块,则以下说法正确的是( )
,现将同样的木块放在光滑的水平桌面上,相同的子弹仍以速度υ沿水平方向射入木块,则以下说法正确的是( )A.若M=3m,则能够射穿木块
B.若M=3m,不能射穿木块,子弹将留在木块中,一起以共同的速度做匀速运动
C.若M=3m,刚好能射穿木块,此时相对速度为零
D.无法确定子弹能否打穿穿木块.因为不知道子弹和木块间作用力大小及木块的厚度
【答案】分析:木块固定时,子弹射穿木块,克服摩擦力做的功等于产生的内能,根据能量守恒列式;木块不固定时,子弹射入木块,系统动量守恒,假设不能穿出,则最后有共同速度,根据动量守恒定律求解出共同速度后,根据功能关系列式求解子弹射入深度,看与假设是否矛盾,从而判断是否射出.
解答:解:A、B、C、木块固定时,子弹射穿木块,设木块长度为d,根据功能关系,有
fd= m
m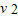 -
- m(
m(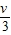 )2
)2
Q= m
m 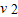 -
- m(
m( 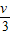 )2
)2
故
fd=Q= m
m
即
f=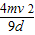 ①
①
木块不固定时,子弹射入木块,系统动量守恒,假设不能穿出;
根据动量守恒定律,有
mv=(M+m)v
根据功能关系,有
Q′=fx= m
m 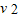 -
- (M+m)v2
(M+m)v2
据题意,有:M=3m
解得
x= ②
②
将①式代入②式,得到
x=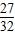 d<d
d<d
故假设成立,子弹不能射出;故A错误,B正确,C错误;
D、由前面解答可知,因为不知道M与m关系,故无法确定子弹能否打穿木块.故D错误;
故选B.
点评:本题关键是对子弹射穿木块过程运用动量守恒和功能关系联立方程求解,然后对结果进行讨论.
解答:解:A、B、C、木块固定时,子弹射穿木块,设木块长度为d,根据功能关系,有
fd=
 m
m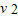 -
- m(
m(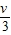 )2
)2Q=
 m
m 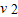 -
- m(
m( 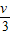 )2
)2故
fd=Q=
 m
m
即
f=
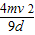 ①
①木块不固定时,子弹射入木块,系统动量守恒,假设不能穿出;
根据动量守恒定律,有
mv=(M+m)v
根据功能关系,有
Q′=fx=
 m
m 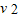 -
- (M+m)v2
(M+m)v2据题意,有:M=3m
解得
x=
 ②
②将①式代入②式,得到
x=
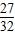 d<d
d<d故假设成立,子弹不能射出;故A错误,B正确,C错误;
D、由前面解答可知,因为不知道M与m关系,故无法确定子弹能否打穿木块.故D错误;
故选B.
点评:本题关键是对子弹射穿木块过程运用动量守恒和功能关系联立方程求解,然后对结果进行讨论.

练习册系列答案
相关题目
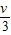 ,现将同样的木块放在光滑的水平桌面上,相同的子弹仍以速度v沿水平方向射入木块,设子弹在木块中所受阻力不变,则以下说法正确的是( )
,现将同样的木块放在光滑的水平桌面上,相同的子弹仍以速度v沿水平方向射入木块,设子弹在木块中所受阻力不变,则以下说法正确的是( )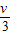 ,现将同样的木块放在光滑的水平桌面上,相同的子弹仍以速度v沿水平方向射入木块.已知木块对子弹阻力大小恒定,且M=3m,则子弹( )
,现将同样的木块放在光滑的水平桌面上,相同的子弹仍以速度v沿水平方向射入木块.已知木块对子弹阻力大小恒定,且M=3m,则子弹( )