题目内容
【题目】如图所示,空间存在着电场强度
、方向竖直向上的匀强电场,在电场内一长为L=0.5m的绝缘细线一端固定于O点,另一端拴着质量m=0.5kg、电荷量
的小球。现将细线拉至水平位置,将小球由静止释放,小球向上运动,当小球运动到最高点时细线受到的拉力恰好达到它能承受的最大值而断裂,取
。求:
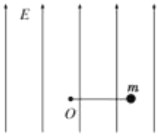
(1)小球运动到圆周最高点的速度；
(2)细线能承受的最大拉力值。
【答案】（1）
m/s（2）15N
【解析】
由小球运动到最高点细线被拉断，则说明电场力竖直向上，再由电场线竖直向上，则可判定小球带正电；设小球运动到最高点时速度为v，对该过程由动能定理有：
（qE-mg）L=
mv2…①
在最高点对小球由牛顿第二定律得：T+mg-qE=m
…②
由①②式解得：T=15N，v＝m/s
练习册系列答案
相关题目
