题目内容
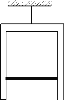
【题目】如图所示,一圆柱形汽缸沿水平方向固定在桌面上,一定量的理想气体被活塞封闭其中。已知汽缸壁导热良好,活塞可沿汽缸壁无摩擦的滑动。开始时气体压强为P,活塞内表面与汽缸底部的距离为L,环境温度为T。现用一条轻绳一端连接活塞,另一端通过定滑轮连接质量为m的物体。在物体的同一位置用另一轻绳连接屋顶,定滑轮也固定在屋顶上,重新平衡后,活塞向右移动h,两绳间的夹角为θ,两绳与水平方向的夹角都相同。不计滑轮的摩擦,重力加速度为g,大气压强不变。求:
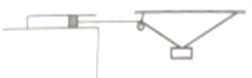
(i)活塞横切的面积;
(ii)剪断右侧的轻绳,重新平衡后,活塞内表面与汽缸底部的距离变为多大?
【答案】(1)![]() (2)
(2)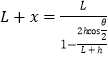
【解析】
(1)分别对物体、活塞列出平衡方程,对气体列出等温变化方程,联立求解活塞的截面积;
(2)剪断右侧轻绳,重新平衡后,对气体列出等温变化方程,联立求解活塞内表面与汽缸底部的距离;
(1)设绳子的拉力为T,则对物体:![]() ;
;
对活塞:T+P1S=PS
对气体:P1S(L+h)=PSL
联立方程可得:![]()
(2)剪断右侧轻绳,重新平衡后,气体的压强变为:![]()
由玻意耳定律可得:![]()
联立得: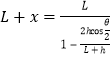

练习册系列答案
相关题目