题目内容
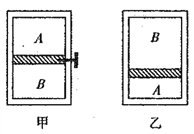
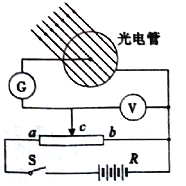
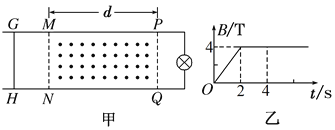
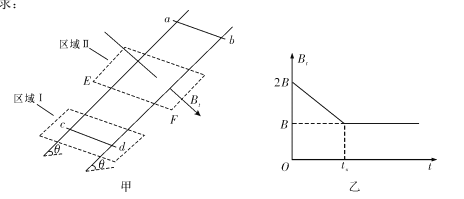
【题目】如图甲所示，间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上。在区域I内有方向垂直于斜面的匀强磁场，磁感应强度恒为B；在区域Ⅱ内有垂直于斜面向下的匀强磁场，其磁感应强度B1的大小随时间t变化的规律如图乙所示。t=0时刻，在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑，同时下端的另一金属细棒cd在位于区域工内的导轨上也由静止释放。在ab棒运动到区域Ⅱ的下边界EF之前，cd棒始终静止不动，两棒均与导轨接触良好。已知cd棒的质量为m、电阻为R，a6棒的质量、阻值均未知，区域Ⅱ沿斜面的长度为2l，在t=tx时刻（tx未知）ab棒恰好进入区域Ⅱ，重力加速度为g。求：
(1)试判断通过cd棒的电流方向和区域工内磁场的方向；
(2)当金属棒ab在区域Ⅱ内运动时，金属棒cd消耗的电功率P；
(3)ab棒开始下滑的位置离区域Ⅱ下边界的距离；
(4)为了求得ab棒开始下滑至EF的过程中，回路中产生总的热量Q，某同学先求出ab棒 的质量、到达EF处的速度，并利用(3)问中的距离，然后用总热量Q等于机械能的减小量进行求解。若这位同学的方法正确，请用他的方法求出总热量Q；若他的方法不正确，请用你的方法求出总热量Q。
【答案】（1）从d到c 区域I内磁场垂直于斜面向上 （2）
（3）
（4）不正确 
【解析】本题考查电磁感应中的单棒问题，涉及楞次定律、法拉第电磁感应定律、平衡、闭合电路欧姆定律等知识的应用。
（1）Ⅱ内磁场均匀变化因此在回路中产生感应电流，由楞次定律可知，流过cd的电流方向是由d到c。
因cd棒静止，由平衡条件可得cd棒所受安培力沿导轨向上，据左手定则可知，区域I内磁场垂直于斜面向上。
（2）因cd棒静止，由平衡条件可得 
金属棒ab在区域Ⅱ内运动时，金属棒cd消耗的电功率
解得
，
（3）ab棒开始下滑到达区域Ⅱ前做匀加速运动，加速度
因在ab棒运动到区域Ⅱ的下边界EF之前，cd棒始终静止不动，则ab棒达区域Ⅱ前后回路中的电动势不变，且ab棒在区域Ⅱ中做匀速直线运动，可得
，即
解得：
、
ab棒开始下滑的位置离区域Ⅱ下边界的距离
（4）这位同学的解法不正确。
正确的解法是：ab棒在区域Ⅱ中运动的时间
ab棒开始下滑至EF的总时间
电路中的电动势
ab棒开始下滑至EF回路中产生总的热量
