题目内容
 早在19世纪,匈牙利物理学家厄缶就明确指出:“沿水平地面向东运动的物体,其重量(即:列车的视重或列车对水平轨道的压力)一定要减轻.”后来,人们常把这类物理现象称为“厄缶效应”.如图所示:我们设想,在地球赤道附近的地平线上,有一列质量是M的列车,正在以速率v,沿水平轨道匀速向东行驶.已知:①地球的半径R;②地球的自转周期T.今天我们象厄缶一样,如果仅考虑地球自转的影响(火车随地球做线速度为2πR/T的圆周运动)时,火车对轨道的压力为N;在此基础上,又考虑到这列火车匀速相对地面又附加了一个线速度v做更快的圆周运动,并设此时火车对轨道的压力为N′,那么单纯地由于该火车向东行驶而引起火车对轨道压力减轻的数量(N-N′)为
早在19世纪,匈牙利物理学家厄缶就明确指出:“沿水平地面向东运动的物体,其重量(即:列车的视重或列车对水平轨道的压力)一定要减轻.”后来,人们常把这类物理现象称为“厄缶效应”.如图所示:我们设想,在地球赤道附近的地平线上,有一列质量是M的列车,正在以速率v,沿水平轨道匀速向东行驶.已知:①地球的半径R;②地球的自转周期T.今天我们象厄缶一样,如果仅考虑地球自转的影响(火车随地球做线速度为2πR/T的圆周运动)时,火车对轨道的压力为N;在此基础上,又考虑到这列火车匀速相对地面又附加了一个线速度v做更快的圆周运动,并设此时火车对轨道的压力为N′,那么单纯地由于该火车向东行驶而引起火车对轨道压力减轻的数量(N-N′)为M[
+2
v]
| v2 |
| R |
| 2π |
| T |
M[
+2
v]
.| v2 |
| R |
| 2π |
| T |
分析:火车做匀速圆周运动,则由向心力公式可求两种情况下火车对地球的压力;求出两力的差值即可得出结论.
解答:解:若仅考虑地球的自转影响时,火车绕地心做圆周运动的线速度大小为
R,以火车为研究对象,根据牛顿第二定律得;Mg-N=M(
)2R;得到N=Mg-M(
)2R;
若这列火车相对地面又附加了一个线速度v,火车绕地心做圆周运动的线速度大小为v+
,根据牛顿第二定律可得:Mg-N′=M
,得到N′=Mg-M
则N-N′=[Mg-M(
)2R]-[Mg-M
]=M[
+2
v]
故答案为:M[
+2
v]
| 2π |
| T |
| 2π |
| T |
| 2π |
| T |
若这列火车相对地面又附加了一个线速度v,火车绕地心做圆周运动的线速度大小为v+
| 2πR |
| T |
(v+
| ||
| R |
(v+
| ||
| R |
则N-N′=[Mg-M(
| 2π |
| T |
(v+
| ||
| R |
| v2 |
| R |
| 2π |
| T |
故答案为:M[
| v2 |
| R |
| 2π |
| T |
点评:本题考查学生的建模能力,注意根据所学知识正确得出合理的模型,才能正确解题.

练习册系列答案
相关题目
 (2009?南通模拟)早在19世纪,匈牙利物理学家厄缶就明确指出:“沿水平地面向东运动的物体,其质量(即:列车的视重或列车对水平轨道的压力)一定要减轻.”后来,人们常把这类物理现象称之为“厄缶效应”.如图所示,我们设想,在地球赤道附近的地平线上,有一列质量是M的列车,正在以速率v沿水平轨道匀速向东行驶.已知:(1)地球的半径R;(2)地球的自转周期T.今天我们像厄缶一样,如果仅仅考虑地球的自转影响(火车随地球做线速度为
(2009?南通模拟)早在19世纪,匈牙利物理学家厄缶就明确指出:“沿水平地面向东运动的物体,其质量(即:列车的视重或列车对水平轨道的压力)一定要减轻.”后来,人们常把这类物理现象称之为“厄缶效应”.如图所示,我们设想,在地球赤道附近的地平线上,有一列质量是M的列车,正在以速率v沿水平轨道匀速向东行驶.已知:(1)地球的半径R;(2)地球的自转周期T.今天我们像厄缶一样,如果仅仅考虑地球的自转影响(火车随地球做线速度为 早在19世纪,匈牙利物理学家厄缶就明确指出:“沿水平地面向东运动的物体,其重量(即:列车的视重或列车对水平轨道的压力)一定会减小.”后来,人们常把这类物理现象称为“厄缶效应”.如图所示:我们设想,在地球赤道附近的地平线上,有一列质量是M的列车,正在以速率v,沿水平轨道匀速向东行驶.已知:
早在19世纪,匈牙利物理学家厄缶就明确指出:“沿水平地面向东运动的物体,其重量(即:列车的视重或列车对水平轨道的压力)一定会减小.”后来,人们常把这类物理现象称为“厄缶效应”.如图所示:我们设想,在地球赤道附近的地平线上,有一列质量是M的列车,正在以速率v,沿水平轨道匀速向东行驶.已知: A.
A.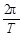 R的圆周运动)时,火车对轨道的压力为N;在此基础上,又考虑到这列火车相对地面又附加了一个线速度v,做更快的匀速圆周运动,并设此时火车对轨道的压力为
R的圆周运动)时,火车对轨道的压力为N;在此基础上,又考虑到这列火车相对地面又附加了一个线速度v,做更快的匀速圆周运动,并设此时火车对轨道的压力为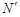 .那么,单纯地由于该火车向东行驶而引起火车对轨道的压力减轻的数量(N-
.那么,单纯地由于该火车向东行驶而引起火车对轨道的压力减轻的数量(N-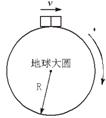
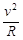 B.M[
B.M[