题目内容
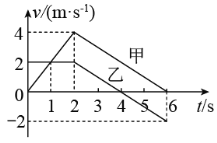
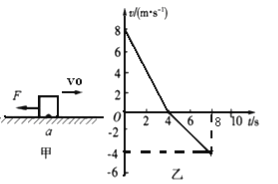
【题目】如图甲,质量![]() 的物体在水平面上向右做直线运动。过a点时给物体作用一个水平向左的恒力F并开始计时,选水平向右为速度的正方向,通过速度传感器测出物体的瞬时速度,所得v-t图像如图乙所示。取重力加速度
的物体在水平面上向右做直线运动。过a点时给物体作用一个水平向左的恒力F并开始计时,选水平向右为速度的正方向,通过速度传感器测出物体的瞬时速度,所得v-t图像如图乙所示。取重力加速度![]()
(1)在0~4s内和4~10s内,求物体加速度大小和方向
(2)求力F的大小和物体与水平面间的动摩擦因数
(3)求10s末物体离a点的距离
(4)8s后撤去拉力F,求物体再过5s后离a点的距离
【答案】(1)物体在0-4s内的加速度的大小为2 m/s2,方向与初速度方向相反;物体在4-10s内的加速度的大小为1m/s2,方向方向与初速度方向相反;
(2)力F的大小为3N,物体与水平面间的动摩擦因数μ为0.05;
(3)10s末物体离a点的距离为2m;
(4)8s后撤去拉力F,物体再过5s离a点的距离为5.75m。
【解析】
(1)在0~4s内物体向右做匀减速直线运动的加速度为a1,则由v-t图得:
加速度大小a1=![]() =-2m/s2 方向与初速度方向相反;
=-2m/s2 方向与初速度方向相反;
4~10s内物体向左做匀加速直线运动的加速度为a2,则由v-t图得:
加速度大小a2=![]() =-1m/s2方向与初速度方向相反
=-1m/s2方向与初速度方向相反
(2)根据牛顿第二定律,有
F+μmg=ma1
F-μmg=ma2
解得:F=3N μ=0.05
(3)设10s末物体离a点的距离为d,d应为v-t图与横轴所围的面积
则:d=![]() ×4×8m
×4×8m![]() ×6×6m=2m,负号表示物体在a点以左;
×6×6m=2m,负号表示物体在a点以左;
(4)8s末物体离a点的距离为d1=![]() ×4×8m
×4×8m![]() ×4×4m=8m 即物体在a点右侧8m处;
×4×4m=8m 即物体在a点右侧8m处;
设撤去拉力F后做匀减速直线运动的加速度大小为a3
根据牛顿第二定律,有:μmg=ma3 得:a3=0.5m/s2
由vt=v0+at可得:物体减速到零的时间t=8s
物体在5s内的位移![]()
则此时物体在a点左侧,距离a点的距离为13.75m-8m=5.75m.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案