题目内容
【题目】质量均为m=0.1kg的两小滑块A、B,相距L=2m、放在足够长的绝缘水平面上,与水平面间的动摩擦因数均为μ=0.2,A带电量为q=+3×10﹣3C,B不带电.在水平面附近空间加有水平向左的匀强电场E=l×102v/m,现同时由静止释放A、B,此后A将与B发生多次碰撞,碰撞时间极短且无机械能损失,A带电量保持不变,B始终不带电,g取10m/s2试求
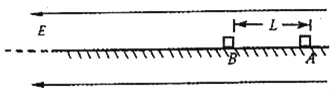
(1)A、B第一次碰前瞬间A的速度vA1
(2)A、B第一次碰后瞬间B的速度vB1
(3)小滑块B运动的总路程S.
【答案】(1)2m/s.(2)2m/s.(3)2m.
【解析】
(1)释放A后的加速度,由牛顿第二定律得:qE﹣μmg=maA
代入得到,aA=1m/s2
又据公式v2A1=2aAL
得到A、B第一次碰前瞬间A的速度vA1=2m/s.
(2)由题,碰撞时间极短且无机械能损失,根据动量和动能守恒得
mvA1=mvA1′+mvB1
![]()
解得:mvA1′=0,vB1=vA1=2m/s,由此可知,碰撞后AB两滑块交换速度.
(3)由于每次碰撞两滑块均交换速度,多次碰撞后,最终A、B停在一起.根据能量守恒定律得 Eq(L+S)=μmg(L+S)+μmgS
解得,S=2m

 夺冠训练单元期末冲刺100分系列答案
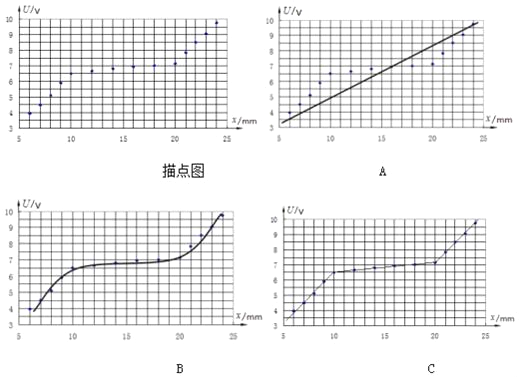
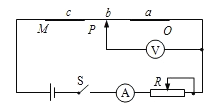
夺冠训练单元期末冲刺100分系列答案【题目】在“探究导体电阻与其影响因素的定量关系”实验中,为了探究3根材料未知,横截面积均为S=0.20mm2的金属丝a、b、c的电阻率,采用如图所示的实验电路.M为金属丝c的左端点,O为金属丝a的右端点,P是金属丝上可移动的接触点.在实验过程中,电流表读数始终为I=1.25A,电压表读数U随OP间距离x的变化如下表:
x/mm | 600 | 700 | 800 | 900 | 1000 | 1200 | 1400 | 1600 | 1800 | 2000 | 2100 | 2200 | 2300 | 2400 |
U/V | 3.95 | 4.50 | 5.10 | 5.90 | 6.50 | 6.65 | 6.82 | 6.93 | 7.02 | 7.15 | 7.85 | 8.50 | 9.05 | 9.75 |
根据实验数据在U﹣x图线上描点如图;三位同学根据U﹣x图线上的描点连线,其中相对最合理的是:_____