题目内容
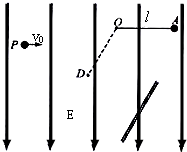 (2010?四川)如图所示,空间有场强E=0.5N/C的竖直向下的匀强电场,长l=0.3
(2010?四川)如图所示,空间有场强E=0.5N/C的竖直向下的匀强电场,长l=0.3| 3 |
| 3 |
(1)求碰撞前瞬间小球P的速度.
(2)若小球C经过路程s=0.09m到达平板,此时速度恰好为0,求所加的恒力.
(3)若施加恒力后,保持平板垂直于纸面且与水平面的夹角不变,在D点下方面任意改变平板位置,小球C均能与平板正碰,求出所有满足条件的恒力.
分析:(1)小球P在碰撞前做类平抛运动,可通过牛顿第二定律求得竖直方向的加速度,再根据时间就可以求得碰撞前小球竖直方向的速度,水平方向速度已知,根据矢量合成求出小球P碰撞瞬间的速度.
(2)小球P与A在D点正碰,小球P此时的速度与水平方向的夹角为θ,连接小球A的绳子与竖直方向的夹角也为θ,可以求得θ,对A球从开始运动至D点的过程,运用动能定理求得A求的速度,再根据动量守恒定理求得碰撞后的共同速度,小球C经过路程s后到达夹板,此时速度变为0,表明小球C一定做匀减速直线运动,由运动学公式得出加速度,再根据牛顿第二定律就可以求出恒力;
(3)平板足够大,且在D点下方任意改变平板位置,那则可以将平板放置到无限远,但根据题意也要发生正碰(垂直打在板上),则小球C必须匀速或匀加速运动.故恒力F′的方向是从竖直向上顺时针转至无限接近速度的方向的范围内,为了使小球C能做匀速直线运动或匀加速直线运动,则在小球C运动的速度的垂直方向上合力为零,即可以求得恒力的范围.
(2)小球P与A在D点正碰,小球P此时的速度与水平方向的夹角为θ,连接小球A的绳子与竖直方向的夹角也为θ,可以求得θ,对A球从开始运动至D点的过程,运用动能定理求得A求的速度,再根据动量守恒定理求得碰撞后的共同速度,小球C经过路程s后到达夹板,此时速度变为0,表明小球C一定做匀减速直线运动,由运动学公式得出加速度,再根据牛顿第二定律就可以求出恒力;
(3)平板足够大,且在D点下方任意改变平板位置,那则可以将平板放置到无限远,但根据题意也要发生正碰(垂直打在板上),则小球C必须匀速或匀加速运动.故恒力F′的方向是从竖直向上顺时针转至无限接近速度的方向的范围内,为了使小球C能做匀速直线运动或匀加速直线运动,则在小球C运动的速度的垂直方向上合力为零,即可以求得恒力的范围.
解答: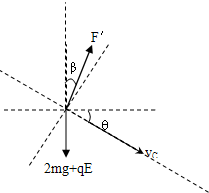
 解:(1)小球P在碰撞前做类平抛运动,竖直方向的加速度
解:(1)小球P在碰撞前做类平抛运动,竖直方向的加速度
a=
=
m/s2=15m/s2
小球P在碰撞瞬间竖直向下的速度为vy=at=15×0.2m/s=3m/s
所以小球P碰撞瞬间的速度vP=
=
m/s=6m/s
(2)小球P与A在D点正碰,小球P此时的速度与水平方向的夹角为θ,连接小球A的绳子与竖直方向的夹角也为θ.tanθ=
=
=
则θ=30°
对A球从开始运动至D点的过程,由动能定理得mglcosθ=
m
解得vA=
=3m/s
P与A球迎面正碰并粘在一起成为小球C,根据动量守恒定律有
mvP-mvA=2mvC
解得:vC=1.5m/s
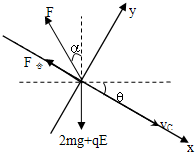
小球C经过路程s后到达夹板,此时速度变为0,表明小球C一定做匀减速直线运动,其运动速度与受力示意图如右图所示.
由运动学公式得:
a=
=12.5m/s2
设恒力F与竖直方向的夹角为α,建立如图所示的坐标系,根据牛顿第二定律得:
在x轴上(沿加速度方向):Fcos(90°-α-θ)-(2mg+qE)sinθ=2ma
在y轴上:Fsin(90°-α-θ)-(2mg+qE)cosθ=0
由以上二式联立并代入数据得:
F=
N,α=30°
(3)平板足够大,且在D点下方任意改变平板位置,那则可以将平板放置到无限远,但根据题意也要发生正碰(垂直打在板上),则小球C必须匀速或匀加速运动.故恒力F′的方向是从竖直向上顺时针转至无限接近速度的方向的范围内,设恒力F′与竖直方向的夹角为β,则有
0°≤β<120°
为了使小球C能做匀速直线运动或匀加速直线运动,则在小球C运动的速度的垂直方向上合力为零,有F'cos(θ-β)=(2mg+qE)cosθ
解得F=
(其中0°≤β<120°).
答:(1)求碰撞前瞬间小球P的速度为;(2)所加的恒力为
N方向与竖直方向夹角为30°;(3)恒力满足的条件为F=
(其中0°≤β<120°).

 解:(1)小球P在碰撞前做类平抛运动,竖直方向的加速度
解:(1)小球P在碰撞前做类平抛运动,竖直方向的加速度a=
| mg+qE |
| m |
| 0.01×10+0.1×0.5 |
| 0.01 |
小球P在碰撞瞬间竖直向下的速度为vy=at=15×0.2m/s=3m/s
所以小球P碰撞瞬间的速度vP=
|
(3
|
(2)小球P与A在D点正碰,小球P此时的速度与水平方向的夹角为θ,连接小球A的绳子与竖直方向的夹角也为θ.tanθ=
| vy |
| v0 |
| 3 | ||
3
|
| ||
| 3 |
则θ=30°
对A球从开始运动至D点的过程,由动能定理得mglcosθ=
| 1 |
| 2 |
| v | 2 A |
解得vA=
| 2glcosθ |
P与A球迎面正碰并粘在一起成为小球C,根据动量守恒定律有
mvP-mvA=2mvC
解得:vC=1.5m/s
小球C经过路程s后到达夹板,此时速度变为0,表明小球C一定做匀减速直线运动,其运动速度与受力示意图如右图所示.
由运动学公式得:
a=
| vC2 |
| 2s |
设恒力F与竖直方向的夹角为α,建立如图所示的坐标系,根据牛顿第二定律得:
在x轴上(沿加速度方向):Fcos(90°-α-θ)-(2mg+qE)sinθ=2ma
在y轴上:Fsin(90°-α-θ)-(2mg+qE)cosθ=0
由以上二式联立并代入数据得:
F=
| ||
| 4 |
(3)平板足够大,且在D点下方任意改变平板位置,那则可以将平板放置到无限远,但根据题意也要发生正碰(垂直打在板上),则小球C必须匀速或匀加速运动.故恒力F′的方向是从竖直向上顺时针转至无限接近速度的方向的范围内,设恒力F′与竖直方向的夹角为β,则有
0°≤β<120°
为了使小球C能做匀速直线运动或匀加速直线运动,则在小球C运动的速度的垂直方向上合力为零,有F'cos(θ-β)=(2mg+qE)cosθ
解得F=
| ||
| 8cos(30°-β) |
答:(1)求碰撞前瞬间小球P的速度为;(2)所加的恒力为
| ||
| 4 |
| ||
| 8cos(30°-β) |
点评:该题涉及的知识点很多,结合了平抛运动的基本规律、运动的合成与分解、动量守恒定律、动能定理、牛顿第二定律的应用等相关知识,难度比较大,对同学们的综合能力要求比较高,属于难题.

练习册系列答案
相关题目
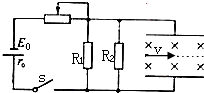 (2010?四川)如图所示,电源电动势E0=15V内阻r0=1Ω,电阻R1=30Ω,R2=60Ω.间距d=0.2m的两平行金属板水平放置,板间分布有垂直于纸面向里、磁感应强度B=1T的匀强磁场.闭合开关S,板间电场视为匀强电场,将一带正电的小球以初速度υ=0.1m/s沿两板间中线水平射入板间.设滑动变阻器接入电路的阻值为Rx,忽略空气对小球的作用,取g=10m/s2.
(2010?四川)如图所示,电源电动势E0=15V内阻r0=1Ω,电阻R1=30Ω,R2=60Ω.间距d=0.2m的两平行金属板水平放置,板间分布有垂直于纸面向里、磁感应强度B=1T的匀强磁场.闭合开关S,板间电场视为匀强电场,将一带正电的小球以初速度υ=0.1m/s沿两板间中线水平射入板间.设滑动变阻器接入电路的阻值为Rx,忽略空气对小球的作用,取g=10m/s2. (2010?四川)a是地球赤道上一栋建筑,b是在赤道平面内作匀速圆周运动、距地面9.6×106m的卫星,c是地球同步卫星,某一时刻b、c刚好位于a的正上方(如图甲所示),经48h,a、b、c的大致位置是图乙中的(取地球半径R=6.4×106m,地球表面重力加速度g=10m/s2,π=
(2010?四川)a是地球赤道上一栋建筑,b是在赤道平面内作匀速圆周运动、距地面9.6×106m的卫星,c是地球同步卫星,某一时刻b、c刚好位于a的正上方(如图甲所示),经48h,a、b、c的大致位置是图乙中的(取地球半径R=6.4×106m,地球表面重力加速度g=10m/s2,π=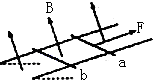 (2010?四川)如图所示,电阻不计的平行金属导轨固定在一绝缘斜面上,两相同的金属导体棒a、b垂直于导轨静止放置,且与导轨接触良好,匀强磁场垂直穿过导轨平面.现用一平行于导轨的恒力F作用在a的中点,使其向上运动.若b始终保持静止,则它所受摩擦力可能( )
(2010?四川)如图所示,电阻不计的平行金属导轨固定在一绝缘斜面上,两相同的金属导体棒a、b垂直于导轨静止放置,且与导轨接触良好,匀强磁场垂直穿过导轨平面.现用一平行于导轨的恒力F作用在a的中点,使其向上运动.若b始终保持静止,则它所受摩擦力可能( ) (2010?四川)如图所示,圆弧虚线表示正点电荷电场的等势面,相邻两等势面间的电势差相等.光滑绝缘直杆沿电场方向水平放置并固定不动,杆上套有一带正电的小滑块(可视为质点),滑块通过绝缘轻弹簧与固定点O相连,并以某一初速度从M点运动到N点,OM<ON.若滑块在M、N时弹簧的弹力大小相等,弹簧始终在弹性限度内,则( )
(2010?四川)如图所示,圆弧虚线表示正点电荷电场的等势面,相邻两等势面间的电势差相等.光滑绝缘直杆沿电场方向水平放置并固定不动,杆上套有一带正电的小滑块(可视为质点),滑块通过绝缘轻弹簧与固定点O相连,并以某一初速度从M点运动到N点,OM<ON.若滑块在M、N时弹簧的弹力大小相等,弹簧始终在弹性限度内,则( )