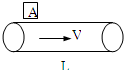题目内容
 如图所示,水平传送皮带顺时针转动,速度大小为2米/秒,现使质量为2千克的工件A以4米/秒的水平速度冲上皮带左端,已知A与皮带间的滑动摩擦系数为μ=0.2,皮带左右长度L=10m,它随皮带运动到右端,则开始时工件A的加速度大小为
如图所示,水平传送皮带顺时针转动,速度大小为2米/秒,现使质量为2千克的工件A以4米/秒的水平速度冲上皮带左端,已知A与皮带间的滑动摩擦系数为μ=0.2,皮带左右长度L=10m,它随皮带运动到右端,则开始时工件A的加速度大小为2
2
m/s2,工件A从左端运动到右端的时间为4.5
4.5
s.分析:对工件A进行受力分析,根据牛顿第二定律求解加速度,判断工件从左到右的运动过程,抓住工件速度不能大于传送带运动速度,分过程求解工件运动时间.
解答:解:对工件进行受力分析有:
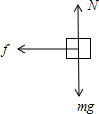
如图工件所受合力F=f=μN=μmg
根据牛顿第二定律F=ma得加速度a=
=μg=2m/s2
因为工件速度大于传送带速度,故在摩擦力作用下工件先做匀减速直线运动,当速度与传送带速度相同时,工件开始匀速直线运动.
根据匀减速直线运动速度时间关系有工件速度减为传送带速度所需要的时间
t1=
=
s=1s
工件位移x1=
×1m=3m
则工件匀速运动的位移为x2=L-x1=7m
匀速运动的时间t2=
=
s=3.5s
所以工件运动的总时间t=t1+t2=4.5s
故答案为:2,4.5

如图工件所受合力F=f=μN=μmg
根据牛顿第二定律F=ma得加速度a=
| F |
| m |
因为工件速度大于传送带速度,故在摩擦力作用下工件先做匀减速直线运动,当速度与传送带速度相同时,工件开始匀速直线运动.
根据匀减速直线运动速度时间关系有工件速度减为传送带速度所需要的时间
t1=
| △v |
| a |
| 4-2 |
| 2 |
工件位移x1=
| 2+4 |
| 2 |
则工件匀速运动的位移为x2=L-x1=7m
匀速运动的时间t2=
| x2 |
| v |
| 7 |
| 2 |
所以工件运动的总时间t=t1+t2=4.5s
故答案为:2,4.5
点评:解决本题的关键理清工件的运动情况,结合牛顿第二定律和运动学公式进行求解

练习册系列答案
相关题目
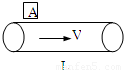
 如图所示,水平传送皮带上的工件A,质量为2千克,它随皮带做匀加速运动,其加速度大小为5米/秒2,若工件与皮带无相对滑动,则工件A受到的静摩擦力方向向
如图所示,水平传送皮带上的工件A,质量为2千克,它随皮带做匀加速运动,其加速度大小为5米/秒2,若工件与皮带无相对滑动,则工件A受到的静摩擦力方向向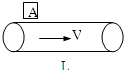 如图所示,水平传送皮带顺时针转动,速度大小为2米/秒,现使质量为2千克的工件A以4米/秒的水平速度冲上皮带左端,已知A与皮带间的滑动摩擦系数为μ=0.2,皮带左右长度L=10m,它随皮带运动到右端,则开始时工件A的加速度大小为________m/s2,工件A从左端运动到右端的时间为________s.
如图所示,水平传送皮带顺时针转动,速度大小为2米/秒,现使质量为2千克的工件A以4米/秒的水平速度冲上皮带左端,已知A与皮带间的滑动摩擦系数为μ=0.2,皮带左右长度L=10m,它随皮带运动到右端,则开始时工件A的加速度大小为________m/s2,工件A从左端运动到右端的时间为________s.