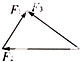题目内容
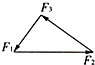
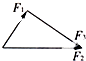
 如图所示,F1、F2、F3和F4为同一水平面内的四个共点力,它们的大小分别是F1=2N、F2=3N、F3=3
如图所示,F1、F2、F3和F4为同一水平面内的四个共点力,它们的大小分别是F1=2N、F2=3N、F3=3| 3 |
分析:建立坐标系:以四个力的作用点为原点,以正东方向为x轴正方向,以正北方向为y轴方向,将F2、F3、F4分解到两个坐标轴上,分别求出x轴和y轴上的合力,再求解四个力的合力的大小和方向.
解答:解: 1、建立坐标系如图.
1、建立坐标系如图.
2、根据平行四边形定则将各力垂直分解到两个坐标轴上.
3、分别求出x轴和y轴上的合力,
x轴方向的合力Fx=F1+F2cos60°+F4cos60°-F3cos30°=1N
y轴方向的合力Fy=F2sin60°+F3sin30°-F4sin60°=
N
所以四个力的合力大小为
F=
=2N,方向东偏北60°.
答:四个力的合力大小为2N,方向东偏北60°.
 1、建立坐标系如图.
1、建立坐标系如图.2、根据平行四边形定则将各力垂直分解到两个坐标轴上.
3、分别求出x轴和y轴上的合力,
x轴方向的合力Fx=F1+F2cos60°+F4cos60°-F3cos30°=1N
y轴方向的合力Fy=F2sin60°+F3sin30°-F4sin60°=
| 3 |
所以四个力的合力大小为
F=
|
答:四个力的合力大小为2N,方向东偏北60°.
点评:正交分解法是求解合力的一种方法,首先要建立坐标系,先正交分解,再求解合力.

练习册系列答案
相关题目
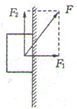 我们把斜向上作用在紧贴竖直静止的物体上的力F分解为如图所示的F1、F2两个分力,则( )
我们把斜向上作用在紧贴竖直静止的物体上的力F分解为如图所示的F1、F2两个分力,则( )| A、F1就是物体对墙的正压力 | B、F1和墙对物体的弹力是作用力反作用力 | C、F1和墙对物体的弹力是一对平衡力 | D、墙对物体的静摩擦力必竖直向下 |
 如图所示,F1、F2是两个互相垂直的共点力,若已知F1的大小为4N,F2的大小为3N,则这两个力的合力F的大小为( )
如图所示,F1、F2是两个互相垂直的共点力,若已知F1的大小为4N,F2的大小为3N,则这两个力的合力F的大小为( ) (2010?金山区一模)如图所示,F1、F2为有一定夹角的两个力,L为过O点的一条直线,当L取什么方向时,F1、F2在L上分力之和为最大( )
(2010?金山区一模)如图所示,F1、F2为有一定夹角的两个力,L为过O点的一条直线,当L取什么方向时,F1、F2在L上分力之和为最大( ) 如图所示,F1、F2、F3、F4四个共点力恰好能用一个正六边形的两条邻边和与它们同顶点的两条对角线表示,且F1=8.0N,则F1和F3的合力大小是
如图所示,F1、F2、F3、F4四个共点力恰好能用一个正六边形的两条邻边和与它们同顶点的两条对角线表示,且F1=8.0N,则F1和F3的合力大小是