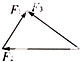题目内容
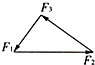
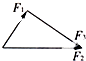
 如图所示,F1、F2、F3、F4四个共点力恰好能用一个正六边形的两条邻边和与它们同顶点的两条对角线表示,且F1=8.0N,则F1和F3的合力大小是
如图所示,F1、F2、F3、F4四个共点力恰好能用一个正六边形的两条邻边和与它们同顶点的两条对角线表示,且F1=8.0N,则F1和F3的合力大小是16
16
N,F2和F3的合力大小是24
24
N.分析:根据平行四边形定则,结合正六边形几何特征,即可求解.
解答:解:由题意可知,正六边形一边的力是8.0N,根据平行四边形定则,可知F3=8
N;
则F1和F3的合力大小,再由平行四边形定则,可得:F13=
=
N=16N,
同理,F2和F3的合力大小F23=8
×
×2N=24N.
故答案为:16,24.
| 3 |
则F1和F3的合力大小,再由平行四边形定则,可得:F13=
|
82+(8
|
同理,F2和F3的合力大小F23=8
| 3 |
| ||
| 2 |
故答案为:16,24.
点评:解决本题的关键知道合力与分力遵循平行四边形定则,在平行四边形定则中,边的长短代表力的大小.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
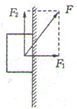 我们把斜向上作用在紧贴竖直静止的物体上的力F分解为如图所示的F1、F2两个分力,则( )
我们把斜向上作用在紧贴竖直静止的物体上的力F分解为如图所示的F1、F2两个分力,则( )| A、F1就是物体对墙的正压力 | B、F1和墙对物体的弹力是作用力反作用力 | C、F1和墙对物体的弹力是一对平衡力 | D、墙对物体的静摩擦力必竖直向下 |
 如图所示,F1、F2是两个互相垂直的共点力,若已知F1的大小为4N,F2的大小为3N,则这两个力的合力F的大小为( )
如图所示,F1、F2是两个互相垂直的共点力,若已知F1的大小为4N,F2的大小为3N,则这两个力的合力F的大小为( ) (2010?金山区一模)如图所示,F1、F2为有一定夹角的两个力,L为过O点的一条直线,当L取什么方向时,F1、F2在L上分力之和为最大( )
(2010?金山区一模)如图所示,F1、F2为有一定夹角的两个力,L为过O点的一条直线,当L取什么方向时,F1、F2在L上分力之和为最大( )