��Ŀ����
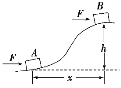
����Ŀ����ͼ����ʾ���߳�ΪL������������ABCD������ֱ���µ���ǿ�糡���糡ǿ��ΪE��������߽�BC���L����ֱ�����㹻���ӫ������ӫ������AB�ӳ��߽���O�㡣����һ����Ϊm�������Ϊ+q�����Ӵ�A����AB������һ���ij��ٽ���糡��ǡ�ô�BC�ߵ��е�P�ɳ�����������������

��1�������ӽ���糡ǰ�ij��ٶȵĴ�С��
��2�������������䣬����糡ǿ��ʹ����ǡ���ܴ�CD�ߵ��е�Q�ɳ��������Ӵ�Q��ɳ�ʱ�Ķ��ܣ�
��3���ֽ��糡����ǿΪE���ֳ�AEFD��EBCF��ͬ�������֣�����EBCF����ƽ��һ�ξ���x��x��L������ͼ����ʾ�������Ӵ���ӫ������λ����0�����y�������y��x�Ĺ�ϵ��
���𰸡���1�����ӽ���糡ǰ�ij��ٶȵĴ�СΪ![]() ��
��
��2�������������䣬����糡ǿ��ʹ����ǡ���ܴ�CD�ߵ��е�Q�ɳ������Ӵ�Q��ɳ�ʱ�Ķ���Ϊ![]() ��
��
��3��y��x�Ĺ�ϵΪ![]() ��
��
��������
����(1)�����ڵ糡������ƽ���˶���ˮƽ����L=v0t����ֱ����![]() ����
����![]() (4��)
(4��)
(2)�����������䣬����糡ǿ�ȣ���CD���е�Q�ɳ����BC���е�P�ɳ���ȣ�ˮƽλ�Ƽ��룬��ֱλ�Ƽӱ���������ƽ���˶�֪ʶ![]() ������ٶ�Ϊԭ��8�����糡ǿ��Ϊԭ��8�����糡������ΪW1=8EqL (2��)
������ٶ�Ϊԭ��8�����糡ǿ��Ϊԭ��8�����糡������ΪW1=8EqL (2��)
���Ӵ�CD���е�Q�ɳ�ʱ�Ķ���
![]() (3��)
(3��)
(3)��EBCF����ƽ��һ�ξ���x�������ڵ糡�е���ƽ���˶��ֳ������֣����糡����������ֱ���˶����켣��ͼ��ʾ��

![]() (vyΪ���糡AEFDʱ��ֱ���������) (1��)
(vyΪ���糡AEFDʱ��ֱ���������) (1��)
![]() (2��) A
(2��) A
![]() (vy��Ϊ���糡EBCFʱ��ֱ���������) (1��)
(vy��Ϊ���糡EBCFʱ��ֱ���������) (1��)
y2=(L-x)tan��2=L-x (2��)
![]() (1��)
(1��)

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
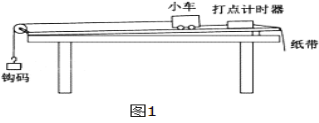
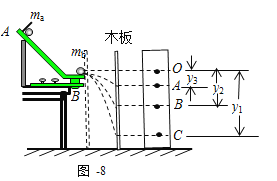
�ۺ��Բ�ϵ�д�����Ŀ��ijͬѧ����̽�������͵����쳤�Ĺ�ϵ��ʵ���У������ͼ����ʾʵ��װ�ã����Ȳ�����ҹ���ʱ���ɵ���Ȼ���ȣ��ٽ�����������ڵ����¶ˣ�ÿ�ζ������Ӧ�ĵ����ܳ��ȣ���������������ı��У�������ʼ���ڵ������ڣ�

�������� | 1 | 2 | 3 | 4 | 5 | 6 |
���ɵ�����СF/N | 0 | 0.49 | 0.98 | 1.47 | 1.96 | 2.45 |
�����ܳ�x/cm | 6 | 7.16 | 8.34 | 9.48 | 10.85 | 11.75 |
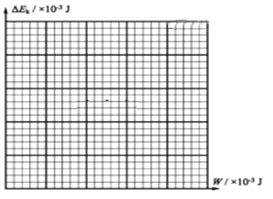
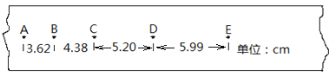
��1������ʵ��������ͼ�ҵ�����ֽ���������ǰ�Ĵβ����ĵ������ܵ�����СF�������ܳ�X֮��ĺ�����ϵ�㣬��ѵ�5��6�β��������ݶ�Ӧ�ĵ��������������F��Xͼ�ߣ�
��2��ͼ�߸������ύ������������� ��
��3���õ��ɵľ���ϵ��k= ��������λ��Ч���֣�