题目内容
8.用自由落体法验证机械能守恒定律的实验中:(1)若实验中所用重锤的质量为m=0.1kg.打点纸带如图1所示,打点时间间隔为0.02s,取B点分析,重锤动能EkB=0.0171J,从开始下落起至B点时重锤的重力势能减少量是0.0172J.(计算结果保留三位有效数字)
(2)根据纸带算出相关各点的速度v,量出对应下落的距离h,则以$\frac{1}{2}$v2为纵轴、以h为横轴作出的图象应是图2中的C.

分析 根据某段时间内的平均速度等于中间时刻的瞬时速度求出B点的速度,从而得出重锤的动能.根据下降的高度求出重力势能的减小量.
根据机械能守恒得出$\frac{1}{2}{v}^{2}$-h的表达式,从而确定正确的图线.
解答 解:(1)B点的速度为:${v}_{B}=\frac{{x}_{AC}}{2T}=\frac{0.0312-0.0078}{0.04}$m/s=0.585m/s,
则B点的动能为:${E}_{kB}=\frac{1}{2}m{{v}_{B}}^{2}=\frac{1}{2}×0.1×0.58{5}^{2}$=0.0171J.
从开始下落起至B点时重锤的重力势能减少量为:△Ep=mgh=0.1×9.8×0.0176J=0.0172J.
(2)根据机械能守恒得:mgh=$\frac{1}{2}m{v}^{2}$,则$\frac{1}{2}{v}^{2}=gh$,可知$\frac{1}{2}{v}^{2}-h$的图线为过原点的倾斜直线,故选:C.
故答案为:(1)0.0171,0.0172; (2)C;
点评 解决本题的关键掌握纸带的处理方法,会通过点迹间的距离求出重力势能的减小量.知道某段时间内的平均速度等于中间时刻的瞬时速度,从而得出动能的大小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.关于下列说法,正确的是( )
| A. | 由欧姆定律I=$\frac{U}{R}$导出R=$\frac{U}{I}$,可知导体的电阻跟导体两端的电压成正比,跟导体中的电流成反比 | |
| B. | 由C=$\frac{Q}{U}$得,电容器的电容与极板所带电荷量成正比,与极板间电势差成反比 | |
| C. | 电源电动势E=$\frac{W}{q}$可知,非静电力做功越多,电源电动势也就越大 | |
| D. | 磁感应强度B=$\frac{F}{IL}$是一个定义式,故B与F、I、L无关,其单位关系是1T=1$\frac{N}{A•m}$ |
16. 如图所示,质量m1=10kg和m2=30kg的两物体叠放在动摩擦因数为0.25的粗糙水平地面上.劲度系数为k=250N/m的轻弹簧处于水平方向,其两端分别与墙壁和质量为m1的物体相连,弹簧处于自然状态.现用一水平拉力F作用于m2上,使它缓慢地向右移动,当移动x=0.20m时,两物体开始相对滑动,取g=10m/s2,则此时水平拉力F的大小为( )
如图所示,质量m1=10kg和m2=30kg的两物体叠放在动摩擦因数为0.25的粗糙水平地面上.劲度系数为k=250N/m的轻弹簧处于水平方向,其两端分别与墙壁和质量为m1的物体相连,弹簧处于自然状态.现用一水平拉力F作用于m2上,使它缓慢地向右移动,当移动x=0.20m时,两物体开始相对滑动,取g=10m/s2,则此时水平拉力F的大小为( )
 如图所示,质量m1=10kg和m2=30kg的两物体叠放在动摩擦因数为0.25的粗糙水平地面上.劲度系数为k=250N/m的轻弹簧处于水平方向,其两端分别与墙壁和质量为m1的物体相连,弹簧处于自然状态.现用一水平拉力F作用于m2上,使它缓慢地向右移动,当移动x=0.20m时,两物体开始相对滑动,取g=10m/s2,则此时水平拉力F的大小为( )
如图所示,质量m1=10kg和m2=30kg的两物体叠放在动摩擦因数为0.25的粗糙水平地面上.劲度系数为k=250N/m的轻弹簧处于水平方向,其两端分别与墙壁和质量为m1的物体相连,弹簧处于自然状态.现用一水平拉力F作用于m2上,使它缓慢地向右移动,当移动x=0.20m时,两物体开始相对滑动,取g=10m/s2,则此时水平拉力F的大小为( )| A. | 50N | B. | 100N | C. | 150N | D. | 200N |
3.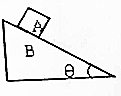 如图所示质量为m的物体A恰好静止在斜面B上,斜面倾角为θ.一同学沿斜面方向对A用力F,B始终静止,设最大静摩擦力等于滑动摩擦力.关于地面对B的静摩擦力f描述正确的是( )
如图所示质量为m的物体A恰好静止在斜面B上,斜面倾角为θ.一同学沿斜面方向对A用力F,B始终静止,设最大静摩擦力等于滑动摩擦力.关于地面对B的静摩擦力f描述正确的是( )
 如图所示质量为m的物体A恰好静止在斜面B上,斜面倾角为θ.一同学沿斜面方向对A用力F,B始终静止,设最大静摩擦力等于滑动摩擦力.关于地面对B的静摩擦力f描述正确的是( )
如图所示质量为m的物体A恰好静止在斜面B上,斜面倾角为θ.一同学沿斜面方向对A用力F,B始终静止,设最大静摩擦力等于滑动摩擦力.关于地面对B的静摩擦力f描述正确的是( )| A. | F沿斜面向上一直增大,f水平向右一直增大 | |
| B. | F沿斜面向上一直增大,f水平向右增大到最大值mgsin2θ | |
| C. | F沿斜面向下一直增大,f水平向左一直增大 | |
| D. | F沿斜面向下一直增大,f一直为零 |
20.电阻R1与R2并联在电路中,通过R1与R2的电流之比为1:3,则当R1与R2串联后接入电路中时,R1和R2两端电压之比U1:U2为( )
| A. | 1:3 | B. | 3:1 | C. | 1:4 | D. | 4:1 |
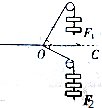
 如图所示,在xOy坐标系中,以(r,0)为圆心,r为半径的圆形区域内存在匀强磁场磁场区域的圆心为O′,磁场的磁感应强度大小为B,方向垂直于纸面向里.在y>r的足够大的区域内,存在沿y轴负方向的匀强电场,场强大小为E.从O点以相同速率向不同方向发射质子,质子的运动轨迹均在纸面内,且质子在磁场中运动的轨迹半径也为r.已知质子的电荷量为q,质量为m,不计质子所受重与及质子间相互作用力的影响.
如图所示,在xOy坐标系中,以(r,0)为圆心,r为半径的圆形区域内存在匀强磁场磁场区域的圆心为O′,磁场的磁感应强度大小为B,方向垂直于纸面向里.在y>r的足够大的区域内,存在沿y轴负方向的匀强电场,场强大小为E.从O点以相同速率向不同方向发射质子,质子的运动轨迹均在纸面内,且质子在磁场中运动的轨迹半径也为r.已知质子的电荷量为q,质量为m,不计质子所受重与及质子间相互作用力的影响.