题目内容
【题目】在“验证动量守恒定律”的实验中:
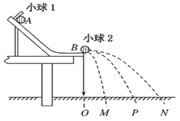
(1)在确定小球落地点的平均位置时通常采用的做法是用圆规画一个尽可能小的圆把所有的落点圈在里面,圆心即平均位置 ,其目的是减小实验中的______________.
(2)入射小球每次必须从斜槽上_______滚下,这是为了保证入射小球每一次到达斜槽末端时速度相同.
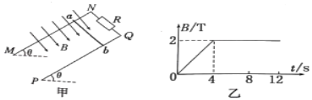
(3)入射小球的质量为![]() ,被碰小球的质量为m2,在m1
,被碰小球的质量为m2,在m1![]() m2时,实验中记下了O、M、P、N四个位置(如图所示),若满足_____________(用m1、m2、OM、OP、ON表示),则说明碰撞中动量守恒;若还满足_________________(只能用OM、OP、ON表示),则说明碰撞前后动能也相等.
m2时,实验中记下了O、M、P、N四个位置(如图所示),若满足_____________(用m1、m2、OM、OP、ON表示),则说明碰撞中动量守恒;若还满足_________________(只能用OM、OP、ON表示),则说明碰撞前后动能也相等.
【答案】用圆规画一个尽可能小的圆把所有的落点圈在里面,圆心即平均位置 偶然误差 同一位置由静止开始 m1·OP=m1·OM+m2·ON OP=ON-OM
【解析】
(1)由于落点比较密集,又较多,每次测量距离很难,确定落点平均位置的方法是最小圆法,用圆规画一个尽可能小的圆把所有的落点圈在里面,圆心即平均位置,这样可以减小偶然误差;
(2)为了保证小球每次到达斜面末端时速度相同,应让小球每次从同一位置由静止滑下;
(3)设落地时间为t,则有:v1=![]() ,v′1=
,v′1=![]() ,v′2=
,v′2=![]()
而动量守恒的表达式是:m1v1=m1v1′+m2v2′
所以若两球相碰前后的动量守恒,则有:m1OM+m2ON=m1OP成立;
若碰撞是弹性碰撞,动能是守恒的,则有:![]() m1v12=
m1v12=![]() m1v1′2+
m1v1′2+![]() m2v2′2
m2v2′2
即m1OM2+m2ON2=m1OP2成立
联立可得:OP=ON-OM;

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目