题目内容
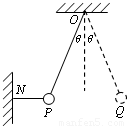
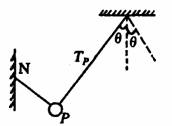
如图所示，细线NP与细线DP把质量为m的小球维持在位置P，OP与竖直方向夹角为θ，NO与OP垂直，这时细线0P中的张力大小为TP，作用于小球的合力大小为FP；若剪断NP，当小球摆到位置Q时，DQ与竖直方向夹角也为θ，细线中张力大小为TQ，作用于小球的合力大小为FQ，则（ ）分析：本题的关键是明确细线NP剪断前小球处于平衡状态，根据平衡条件可求出拉力和合力大小；剪断细线NP后，小球将会做圆周运动至Q点时，小球所受的合力不为零，应根据牛顿第二定律结合向心力公式求出拉力和合力．
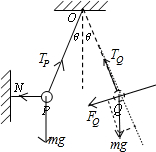
解答：解：剪断细线NP前，对球受力分析如图所示，根据平衡条件可得
=
，
=0
剪断细线后，小球在Q点时受力分析如图所示，由能量守恒定律可知，小球在Q点时的速度应为零，根据牛顿第二定律应有：
-mgcosθ=0，
=mgsinθ
解得
=mgcosθ，
=mgsinθ，可见
，
，所以D正确．
故选D．
| T | P |
| mg |
| cosθ |
| F | P |
剪断细线后，小球在Q点时受力分析如图所示，由能量守恒定律可知，小球在Q点时的速度应为零，根据牛顿第二定律应有：
| T | Q |
| F | Q |
解得
| T | Q |
| F | Q |
| T | P |
| ≠T | Q |
| F | P |
| ≠F | Q |
故选D．
点评：要熟记结论：做圆周运动的物体所受的指向圆心方向的合力等于向心力．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
如图所示，水平细线NP与斜拉细线OP把质量为m的小球维持在位置P，OP与竖直方向夹角为θ，这时斜拉细线中的张力为TP，作用于小球的合力为FP；若剪断NP，当小球摆到位置Q时，OQ与竖直方向夹角也为θ，细线中的张力为TQ，作用于小球的合力为FQ，则（ ）
