题目内容
(20分)如图所示,水平虚线X下方区域分布着方向水平、垂直纸面向里、磁感应强度为B的匀强磁场,整个空间存在匀强电场(图中未画出)。质量为m,电荷量为+q的小球P静止于虚线X上方A点,在某一瞬间受到方向竖直向下、大小为I的冲量作用而做匀速直线运动。在A点右下方的磁场中有定点O,长为l的绝缘轻绳一端固定于O点,另一端连接不带点的质量同为m的小球Q,自然下垂。保持轻绳伸直,向右拉起Q,直到绳与竖直方向有一小于5。的夹角,在P开始运动的同时自由释放Q,Q到达O点正下方W点是速率为v0。P、Q两小球在W点发生正碰,碰到电场,磁场消失,两小球黏在一起运动。P、Q两小球均视为质点,P小球的电荷量保持不变,绳不可伸长不计空气阻力,重力加速度为g。

(1)求匀强电场场强 的大小和
的大小和 进入磁场时的速率
进入磁场时的速率 ;
;
(2)若绳能承受的最大拉力为 ,要使绳不断,
,要使绳不断, 至少为多大?
至少为多大?
(3)求 点距虚线
点距虚线 的距离
的距离
【答案】
(1)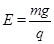
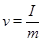 (2)
(2)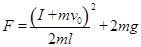
(3)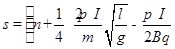 (n为大于(
(n为大于(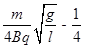 )的整数)
)的整数)
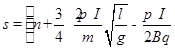 (n为大于(
(n为大于(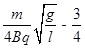 )的整数)
)的整数)
【解析】(1)设小球P受到电场力为F1,
则有F1=qE,在整个空间里有电场力和重力平衡所以有F1=mg
得到: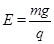
设小球P受到冲量后速度为V由动量定理可得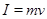
解得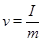
(2)设P、Q同向相碰后在W点的最大速度为Vm,
由动量守恒定律得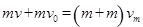
此刻绳子张力最大,由牛顿第二定律可得: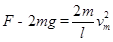
联立方程可得: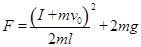
(3)设P在X上方做匀速直线运动的时间为tp1,则有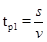
在磁场中做圆周运动的时间为tp2,则有: 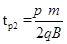
设小球Q从开始运动到与小球P反向相碰的时间为tQ,
由单摆的周期性可知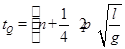
由题意可知: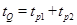
联立方程可得: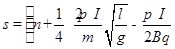 (n为大于(
(n为大于(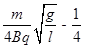 )的整数)
)的整数)
设小球Q从开始运动到与小球P同向向相碰的时间为iQ,
由单摆的周期性可知: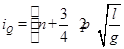
同理可得: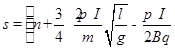 (n为大于(
(n为大于(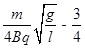 )的整数)
)的整数)

练习册系列答案
相关题目
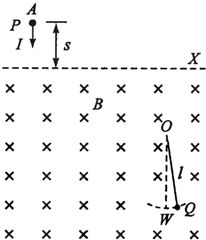 如图所示,水平虚线X下方区域分布着方向水平、垂直纸面向里、磁感应强度为B的匀强磁场,整个空间存在匀强电场(图中未画出).质量为m,电荷量为+q的小球P静止于虚线X上方A点,在某一瞬间受到方向竖直向下、大小为I的冲量作用而做匀速直线运动.在A点右下方的磁场中有定点O,长为l的绝缘轻绳一端固定于O点,另一端连接不带电的质量同为m的小球Q,自然下垂.保持轻绳伸直,向右拉起Q,直到绳与竖直方向有一小于50的夹角,在P开始运动的同时自由释放Q,Q到达O点正下方W点时速率为v0.P、Q两小球在W点发生正碰,碰后电场、磁场消失,两小球粘在一起运动.P、Q两小球均视为质点,P小球的电荷量保持不变,绳不可伸长,不计空气阻力,重力加速度为g.
如图所示,水平虚线X下方区域分布着方向水平、垂直纸面向里、磁感应强度为B的匀强磁场,整个空间存在匀强电场(图中未画出).质量为m,电荷量为+q的小球P静止于虚线X上方A点,在某一瞬间受到方向竖直向下、大小为I的冲量作用而做匀速直线运动.在A点右下方的磁场中有定点O,长为l的绝缘轻绳一端固定于O点,另一端连接不带电的质量同为m的小球Q,自然下垂.保持轻绳伸直,向右拉起Q,直到绳与竖直方向有一小于50的夹角,在P开始运动的同时自由释放Q,Q到达O点正下方W点时速率为v0.P、Q两小球在W点发生正碰,碰后电场、磁场消失,两小球粘在一起运动.P、Q两小球均视为质点,P小球的电荷量保持不变,绳不可伸长,不计空气阻力,重力加速度为g.
 的大小和
的大小和 进入磁场时的速率
进入磁场时的速率 ;
; ,要使绳不断,
,要使绳不断, 点距虚线
点距虚线 的距离
的距离

