题目内容
蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目.一个质量m=60kg的运动员,从离水平网面h=3.2m高处自由下落,着网后沿竖直方向蹦回到离水平网面H=5.0m高处.已知运动员与网接触的时间为t=1.2s.现用一简化模型模拟以上过程并进行有关计算:如图a,一个小球从高h处自由下落到弹性支持面上,然后小球在弹性支持面上下陷一段距离x,速度恰为零(如图b).紧接着弹性支持面逐渐恢复,同时小球内携带的轻弹簧弹出,当弹簧弹出的长度等于△x时,弹性面和弹簧均恰好处于自然状态.假设弹簧力以及弹性支持面的力均为恒力,g=10m/s2.求:
(1)运动员从h高处自由下落到弹性支持面上时的运动速度多大?
(2)运动员在与蹦床接触过程中的加速度多大?
(3)蹦床对运动员的作用力多大?

【答案】分析:(1)运动员做自由落体运动,直接根据机械能守恒定律列式求解;
(2)根据题意,运动员与蹦床接触过程是先减速下降后加速上升,整个过程是匀变速过程,根据运动学公式结合几何关系列式后联立求解;
(3)对运动员受力分析,然后根据牛顿第二定律列式求解.
解答:(1)由 ,得
,得
 =8m/s
=8m/s
即运动员从h高处自由下落到弹性支持面上时的运动速度是8m/s.
(2)设运动员的加速度为a,最大速度为v2,根据运动学公式结合几何关系,有
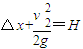
其中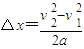 )
)
又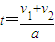
可解得:a=14.4m/s2
即运动员在与蹦床接触过程中的加速度为14.4m/s2.
(3)运动员受重力和支持力,根据牛顿第二定律,有
F-mg=ma
得F=1464N
即蹦床对运动员的作用力为1464N.
点评:本题关键是对运动员的各个运动情况分析清楚,然后结合机械能守恒定律、运动学公式、牛顿第二定律和几何关系列式后联立求解.
(2)根据题意,运动员与蹦床接触过程是先减速下降后加速上升,整个过程是匀变速过程,根据运动学公式结合几何关系列式后联立求解;
(3)对运动员受力分析,然后根据牛顿第二定律列式求解.
解答:(1)由
 ,得
,得 =8m/s
=8m/s即运动员从h高处自由下落到弹性支持面上时的运动速度是8m/s.
(2)设运动员的加速度为a,最大速度为v2,根据运动学公式结合几何关系,有
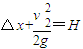
其中
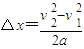 )
)又
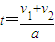
可解得:a=14.4m/s2
即运动员在与蹦床接触过程中的加速度为14.4m/s2.
(3)运动员受重力和支持力,根据牛顿第二定律,有
F-mg=ma
得F=1464N
即蹦床对运动员的作用力为1464N.
点评:本题关键是对运动员的各个运动情况分析清楚,然后结合机械能守恒定律、运动学公式、牛顿第二定律和几何关系列式后联立求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目.一个运动员从高处自由落下,以v1=6m/s的竖直速度着网,与网作用后,沿着竖直方向以v2=8m/s的速度弹回.已知运动员与网接触的时间为△t=1.0s.那么运动员在与网接触的这段时间内平均加速度的大小和方向分别为( )
| A、14m/s2,竖直向上 | B、14m/s2,竖直向下 | C、2m/s2,竖直向上 | D、2m/s2,竖直向下 |
 蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目(如图所示).一个质量为 60kg 的运动员,从离水平网面 3.2m 高处自由下落,着网后沿竖直方向蹦回到离水平网面 5.0m 高处.已知运动员与网接触的时间为 1.2s.若把在这段时间内网对运动员的作用力当作恒力处理,求此力的大小.(g=10m/s2)
蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目(如图所示).一个质量为 60kg 的运动员,从离水平网面 3.2m 高处自由下落,着网后沿竖直方向蹦回到离水平网面 5.0m 高处.已知运动员与网接触的时间为 1.2s.若把在这段时间内网对运动员的作用力当作恒力处理,求此力的大小.(g=10m/s2) (2011?椒江区模拟)蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目.一个质量m=60kg的运动员,从离水平网面h=3.2m高处自由下落,着网后沿竖直方向蹦回到离水平网面H=5.0m高处.已知运动员与网接触的时间为t=1.2s.现用一简化模型模拟以上过程并进行有关计算:
(2011?椒江区模拟)蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目.一个质量m=60kg的运动员,从离水平网面h=3.2m高处自由下落,着网后沿竖直方向蹦回到离水平网面H=5.0m高处.已知运动员与网接触的时间为t=1.2s.现用一简化模型模拟以上过程并进行有关计算: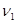 =8m/s的竖直速度触网,与网作用后,沿着竖直方向以
=8m/s的竖直速度触网,与网作用后,沿着竖直方向以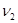 =10m/s的速度弹回。已知运动员与网接触的时间为
=10m/s的速度弹回。已知运动员与网接触的时间为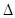 t=1.2s。那么运动员在与网接触的这段时间内平均加速度的大小和方向分别为 ( )
t=1.2s。那么运动员在与网接触的这段时间内平均加速度的大小和方向分别为 ( )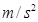 ,向上
,向上