Question

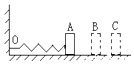
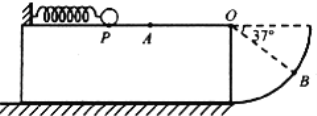
【题目】一个半径为R的圆周的轨道，O点为圆心，B为轨道上的一点，OB与水平方向的夹角为37°．轨道的左侧与一固定光滑平台相连，在平台上一轻质弹簧左端与竖直挡板相连，弹簧原长时右端在A点．现用一质量为m的小球（与弹簧不连接）压缩弹簧至P点后释放．已知重力加速度为g，不计空气阻力．

（1）若小球恰能击中B点，求刚释放小球时弹簧的弹性势能；

（2）试通过计算判断小球落到轨道时速度会否与圆弧垂直；

（3）改变释放点的位置，求小球落到轨道时动能的最小值．

Answer 1

【答案】（1）（2）见解析；（3）

【解析】

试题分析：（1）小球离开O点做平抛运动，设初速度为v0，由

Rcos37°=v0t

解得

由机械能守恒

（2）设落点与O点的连线与水平方向的夹角为θ，小球做平抛运动，由

Rcosθ=v0t

位移方向与圆弧垂直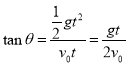

设速度方向与水平方向的夹角为α

所以小球不能垂直击中圆弧

（3）设落地点与O点的连线与水平方向的夹角为θ，小球做平抛运动，

Rcosθ=v0t

由动能定理

解得当时，取最小值