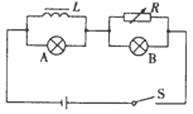
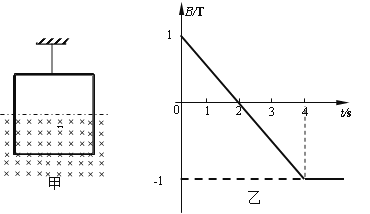
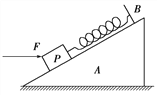
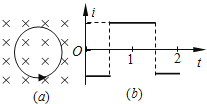
��Ŀ����
����Ŀ��Ϊ��ػ�����������ʻ���������ͷ�ﳣ��װ���Զ������ǣ��Զ��������г���������ͽ���װ�ã���ͼ��ʾ��B�ǹ̶��IJ����ǣ�AΪ�������������335m��ijʱ��B������������ͬʱ����A��Cλ���ɾ�ֹ��ʼ���ȼ���ֱ���˶����������˶���Dλ��ʱ���ܲ��������䳬�������������˶���Eλ��ʱB���յ���������ij������źţ���ʱA��B���355m����֪����Ϊ340m/s��
��1��������C��D��ʱ��TCD����D��E��ʱ��TDE�кι�ϵ���������TCDΪ���٣�
��2���������˶���D����ٶȴ�С
��3���������˶��ļ��ٶȴ�С��
���𰸡�
��1���⣺������������ʱ����ȣ���TCD=TDE
sCE=sBE��sBC=20m
sCD��sDE=1��3
![]()
������C�˶���D��ʱ�伴��������B��D��ʱ�� ![]()
��������C��D��ʱ��TCD����D��E��ʱ��TDE��ϵΪTCD=TDE��TCDΪ1s
��2��DΪCE��ʱ���е㣬���� ![]()
�������˶���D����ٶȴ�СΪ10m/s
��3�������ļ��ٶ�Ϊ ![]()
���������˶��ļ��ٶȴ�СΪ10m/s2��
����������B���������������յ���������ij������ź����ʱ���ڣ����A��λ�ƣ����ڳ�������B������A�뱻A���䵽��B���������ʱ����ȣ������ȱ���ֱ���˶������������������B������A���ʱ����A��λ�ƣ��Ӷ��ó���������B��A��λ�ƣ���������������е�ʱ�䣬�Ӷ��ٸ��ݡ�x=aT2��������˶��ļ��ٶȣ�
�����㾫�����������⣬������Ҫ�˽��ȱ����˶��е�ƽ���ٶ�(ƽ���ٶȣ�V=V0+Vt)��

 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�