题目内容
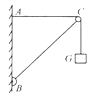
【题目】节水喷灌示意图如图所示，喷口距地面h高，将水水平喷出，其喷灌半径可达8h，时间t内喷出水的质量为m，所用的水是水泵从地下3h深的井里抽取．设水以相同的速率从喷口喷出，水泵效率为η，不计空气阻力，试求：
（1）水从喷口喷出的初速度v；
（2）水泵每分钟对水做的功W；
（3）带动水泵的电动机的最小输出功率P．
【答案】
（1）解：水从喷口喷出后做平抛运动，设平抛运动的时间为t′，则有：
，
8h=vt′，
联立解得：v= 
．
答：水从喷口喷出的初速度v为 ；
（2）解：设时间t内喷出水的动能为Ek，水获得的重力势能为Ep，水泵对水所做的功用于增加水的动能和重力势能，则有：
动能为： 
，
重力势能为：Ep=mg（h+3h）=4mgh，
则有：W=Ek+Ep=16mgh+4mgh=20mgh．
答：水泵每分钟对水做的功为20mgh；
（3）解：带动水泵的电动机的最小输出功率等于水泵的输入功率为：η= 
，
又P= 
，
解得：P= 
．
答：带动水泵的电动机的最小输出功率为 ．
【解析】（1）根据平抛运动的高度求出平抛运动的时间，结合水平位移和时间求出水从喷口喷出的初速度．（2）抓住水泵对水做功等于水获得动能和重力势能，结合能量守恒求出水泵每分钟对水做的功．（3）根据有用功和水泵的效率求出总功，结合功率公式求出最小输出功率．
【考点精析】解答此题的关键在于理解平抛运动的相关知识，掌握特点:①具有水平方向的初速度;②只受重力作用，是加速度为重力加速度g的匀变速曲线运动；运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动，以及对电功率和电功的理解，了解电流做功的实质是电场力对电荷做功.电场力对电荷做功，电荷的电势能减少，电势能转化为其他形式的能.因此电功W=qU=UIt，这是计算电功普遍适用的公式. ? 单位时间内电流做的功叫电功率，P=W/t=UI，这是计算电功率普遍适用的公式．
