题目内容
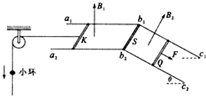 (2011?四川)如图所示,间距l=0.3m的平行金属导轨a1b1c1和a2b2c2分别固定在两个竖直面内,在水平面a1b1b2a2区域内和倾角θ=37°的斜面c1b1b2c2区域内分别有磁感应强度B1=0.4T、方向竖直向上和B2=1T、方向垂直于斜面向上的匀强磁场.电阻R=0.3Ω、质量m1=0.1kg、长为l的相同导体杆K、S、Q分别放置在导轨上,S杆的两端固定在b1、b2点,K、Q杆可沿导轨无摩擦滑动且始终接触良好.一端系于K杆中点的轻绳平行于导轨绕过轻质滑轮自然下垂,绳上穿有质量m2=0.05kg的小环.已知小环以a=6m/s2的加速度沿绳下滑,K杆保持静止,Q杆在垂直于杆且沿斜面向下的拉力F作用下匀速运动.不计导轨电阻和滑轮摩擦,绳不可伸长.取g=10m/s2,sin37°=0.6,cos37°=0.8.求
(2011?四川)如图所示,间距l=0.3m的平行金属导轨a1b1c1和a2b2c2分别固定在两个竖直面内,在水平面a1b1b2a2区域内和倾角θ=37°的斜面c1b1b2c2区域内分别有磁感应强度B1=0.4T、方向竖直向上和B2=1T、方向垂直于斜面向上的匀强磁场.电阻R=0.3Ω、质量m1=0.1kg、长为l的相同导体杆K、S、Q分别放置在导轨上,S杆的两端固定在b1、b2点,K、Q杆可沿导轨无摩擦滑动且始终接触良好.一端系于K杆中点的轻绳平行于导轨绕过轻质滑轮自然下垂,绳上穿有质量m2=0.05kg的小环.已知小环以a=6m/s2的加速度沿绳下滑,K杆保持静止,Q杆在垂直于杆且沿斜面向下的拉力F作用下匀速运动.不计导轨电阻和滑轮摩擦,绳不可伸长.取g=10m/s2,sin37°=0.6,cos37°=0.8.求(1)小环所受摩擦力的大小;
(2)Q杆所受拉力的瞬时功率.
分析:(1)已知物体的加速度,则由牛顿第二定律可求得摩擦力;
(2)对k杆由受力平衡可得出安培力与摩擦力的关系;由电路的规律可得出总电流与k中电流的关系;Q杆的滑动产生电动势,则由E=Blv及闭合电路的欧姆定律可得出电流表达式;由Q杆受力平衡可得出拉力及安培力的表达式,则由功率公式可求得拉力的瞬时功率.
(2)对k杆由受力平衡可得出安培力与摩擦力的关系;由电路的规律可得出总电流与k中电流的关系;Q杆的滑动产生电动势,则由E=Blv及闭合电路的欧姆定律可得出电流表达式;由Q杆受力平衡可得出拉力及安培力的表达式,则由功率公式可求得拉力的瞬时功率.
解答:解:(1)设小环受到的摩擦力大小为Ff,由牛顿第二定律,有
m2g-Ff=m2a
代入数据得
Ff=0.2N;
(2)设通过K杆的电流为I1,K杆受力平衡,有
Ff=B1I1l
设回路中电流为I,总电阻为R总,有:
I=2I1
R总=
R
设Q杆下滑速度大小为v,产生的感应电动势为E,有
I=
E=B2lv
F+m1gsinθ=B2Il
拉力的瞬时功率为
P=Fv
联立以上方程,代入数据解得
Q杆受拉力的功率P=2W.
m2g-Ff=m2a
代入数据得
Ff=0.2N;
(2)设通过K杆的电流为I1,K杆受力平衡,有
Ff=B1I1l
设回路中电流为I,总电阻为R总,有:
I=2I1
R总=
| 3 |
| 2 |
设Q杆下滑速度大小为v,产生的感应电动势为E,有
I=
| E |
| R总 |
E=B2lv
F+m1gsinθ=B2Il
拉力的瞬时功率为
P=Fv
联立以上方程,代入数据解得
Q杆受拉力的功率P=2W.
点评:本题考查切割产生的感应电动势与电路的结合及功能关系的结合,在分析中要注意物体运动状态(加速、匀速或平衡)由牛顿第二定律可得出对应的表达式,从而联立求解.

练习册系列答案
相关题目
 (2011?四川)如图是“神舟”系列航天飞船返回舱返回地面的示意图,假定其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆,需点燃返回舱的缓冲火箭,在火箭喷气过程中返回舱做减速直线运动,则( )
(2011?四川)如图是“神舟”系列航天飞船返回舱返回地面的示意图,假定其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆,需点燃返回舱的缓冲火箭,在火箭喷气过程中返回舱做减速直线运动,则( )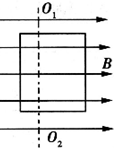 (2011?四川)如图所示,在匀强磁场中匀速转动的矩形线圈的周期为T,转轴O1O2垂直于磁场方向,线圈电阻为2Ω.从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1A.那么( )
(2011?四川)如图所示,在匀强磁场中匀速转动的矩形线圈的周期为T,转轴O1O2垂直于磁场方向,线圈电阻为2Ω.从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1A.那么( )
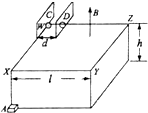 (2011?四川)如图所示:正方形绝缘光滑水平台面WXYZ边长l=1.8m,距地面h=0.8m.平行板电容器的极板CD间距d=0.1m且垂直放置于台面,C板位于边界WX上,D板与边界WZ相交处有一小孔.电容器外的台面区域内有磁感应强度B=1T、方向竖直向上的匀强磁场.电荷量q=5×10-13C的微粒静止于W处,在CD间加上恒定电压U=2.5V,板间微粒经电场加速后由D板所开小孔进入磁场(微粒始终不与极板接触),然后由XY边界离开台面.在微粒离开台面瞬时,静止于X正下方水平地面上A点的滑块获得一水平速度,在微粒落地时恰好与之相遇.假定微粒在真空中运动、极板间电场视为匀强电场,滑块视为质点,滑块与地面间的动摩擦因数μ=0.2,取g=10m/s2
(2011?四川)如图所示:正方形绝缘光滑水平台面WXYZ边长l=1.8m,距地面h=0.8m.平行板电容器的极板CD间距d=0.1m且垂直放置于台面,C板位于边界WX上,D板与边界WZ相交处有一小孔.电容器外的台面区域内有磁感应强度B=1T、方向竖直向上的匀强磁场.电荷量q=5×10-13C的微粒静止于W处,在CD间加上恒定电压U=2.5V,板间微粒经电场加速后由D板所开小孔进入磁场(微粒始终不与极板接触),然后由XY边界离开台面.在微粒离开台面瞬时,静止于X正下方水平地面上A点的滑块获得一水平速度,在微粒落地时恰好与之相遇.假定微粒在真空中运动、极板间电场视为匀强电场,滑块视为质点,滑块与地面间的动摩擦因数μ=0.2,取g=10m/s2