题目内容
7. 摩天轮顺时针匀速转动时,重为G的游客经过图中a、b、c、d四处时,座椅对其竖直方向的支持力大小分别为Na、Nb、Nc、Nd,则( )
摩天轮顺时针匀速转动时,重为G的游客经过图中a、b、c、d四处时,座椅对其竖直方向的支持力大小分别为Na、Nb、Nc、Nd,则( )| A. | Na<G | B. | Nb>G | ||
| C. | 摩天轮匀速转动越快,Nc越大 | D. | 游客在d位置处于失重状态 |
分析 摩天轮顺时针匀速转动时,游客也做匀速圆周运动,靠合力提供向心力,根据牛顿第二定律比较支持力的大小.
解答 解:AB、在a点,根据牛顿第二定律得,G-Na=m$\frac{{v}^{2}}{R}$,知Na<G.在b、d两点,合力方向指向圆心,知竖直方向上的合力为零,则Nb=Nd=G.故A正确,B错误;
C、在c点,根据牛顿第二定律得,Nc-G=m$\frac{{v}^{2}}{R}$,知Nc=m$\frac{{v}^{2}}{R}$+G,故速度越大,Nc越大,故C正确;
D、游客在d点受重力、弹力及拉力的作用,竖直方向合力等于0,故不可能失重,故D错误;
故选:AC
点评 解决本题的关键搞清向心力的来源,运用牛顿第二定律进行求解.对于超重或失重只需分析加速度的大小及方向即可.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
17. 如图所示,质量相同的两小球a、b分别从斜面顶端A和斜面中点B沿水平方向抛出,都恰好落在斜面底端,不计空气阻力,则( )
如图所示,质量相同的两小球a、b分别从斜面顶端A和斜面中点B沿水平方向抛出,都恰好落在斜面底端,不计空气阻力,则( )
 如图所示,质量相同的两小球a、b分别从斜面顶端A和斜面中点B沿水平方向抛出,都恰好落在斜面底端,不计空气阻力,则( )
如图所示,质量相同的两小球a、b分别从斜面顶端A和斜面中点B沿水平方向抛出,都恰好落在斜面底端,不计空气阻力,则( )| A. | 小球a、b沿水平方向抛出的初速度之比为2:1 | |
| B. | 小球a、b离开斜面的最大距离之比为2:1 | |
| C. | 小球a、b到达斜面底端时的动能之比为4:1 | |
| D. | 小球a、b在空中飞行的时间之比为2:1 |
15.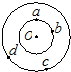 如图所示,两个等量异种点电荷对称地放在一无限大平面的两侧(两点电荷未画出),O点是两点电荷连线与平面的交点,也是连线的中点.在平面内以O点为圆心画两个同心圆,两圆上分别有a、b、c、d四个点,则以下说法正确的是( )
如图所示,两个等量异种点电荷对称地放在一无限大平面的两侧(两点电荷未画出),O点是两点电荷连线与平面的交点,也是连线的中点.在平面内以O点为圆心画两个同心圆,两圆上分别有a、b、c、d四个点,则以下说法正确的是( )
 如图所示,两个等量异种点电荷对称地放在一无限大平面的两侧(两点电荷未画出),O点是两点电荷连线与平面的交点,也是连线的中点.在平面内以O点为圆心画两个同心圆,两圆上分别有a、b、c、d四个点,则以下说法正确的是( )
如图所示,两个等量异种点电荷对称地放在一无限大平面的两侧(两点电荷未画出),O点是两点电荷连线与平面的交点,也是连线的中点.在平面内以O点为圆心画两个同心圆,两圆上分别有a、b、c、d四个点,则以下说法正确的是( )| A. | a、c两点电场强度大小相等 | |
| B. | 若某个检验电荷只在此电场的电场力作用下运动到c点和d点时,加速度大小一定相等 | |
| C. | 带正电的检验电荷从a点在平面内移动到d点电势能一定不变 | |
| D. | 检验电荷可以仅在此电场的电场力作用下在此平面内做匀速圆周运动 |
2.以下说法错误的是( )
| A. | 卫星越往高的地方发射所需要的速度越大,但越高的卫星运行速度越慢 | |
| B. | 同一位置方向上,以较大速度发射卫星所得到的最终运行速度比以较小速度发射所得到的大 | |
| C. | 越高处的卫星速度越慢,因此可以通过加速来降低高度 | |
| D. | 以第三宇宙速度发射,卫星也能逃离地球的引力 |
19.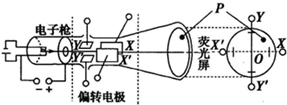 如图所示,示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成.如果在荧光屏上P点出现亮斑,那么示波管中的( )
如图所示,示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成.如果在荧光屏上P点出现亮斑,那么示波管中的( )
 如图所示,示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成.如果在荧光屏上P点出现亮斑,那么示波管中的( )
如图所示,示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成.如果在荧光屏上P点出现亮斑,那么示波管中的( )| A. | 极板X应带正电 | B. | 极板X′应带正电 | C. | 极板Y应带负电 | D. | 极板Y′应带负电 |
16.两球A、B在光滑水平面上沿同一直线,同一方向运动,mA=1kg,mB=2kg,vA=6m/s,vB=2m/s.当A追上B并发生碰撞后,两球A、B速度的可能值是( )
| A. | vA′=5m/s,vB′=2.5m/s | B. | vA′=2m/s,vB′=4m/s | ||
| C. | vA′=-4m/s,vB′=3m/s | D. | vA′=-2m/s,vB′=6m/s |
17.质量2kg的物体从倾角为30°、长4m的光滑斜面顶端由静止开始下滑,若选初始位置为零势能点,g取10m/s2.那么,当它滑到斜面中点时具有的机械能和重力势能分别是( )
| A. | 0,-20J | B. | 80J,-40J | C. | 0,20J | D. | 80J,40J |
 如图所示,在方向水平的匀强电场中,一根不可伸长的绝缘细线的一端固定于O点,另一端连着一个质量为m的带电小球,把小球拉起直至细线与场强平行,然后无初速释放,已知小球摆到最低点的另一侧,线与垂直方向的最大夹角为θ,重力加速度为g,求:
如图所示,在方向水平的匀强电场中,一根不可伸长的绝缘细线的一端固定于O点,另一端连着一个质量为m的带电小球,把小球拉起直至细线与场强平行,然后无初速释放,已知小球摆到最低点的另一侧,线与垂直方向的最大夹角为θ,重力加速度为g,求: