题目内容
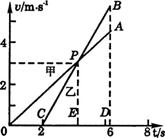
甲、乙两车从同地点出发同向运动,其v-t图象如图2-7-1所示,试计算:
图2-7-1
(1)从乙车开始运动多少时间后两车相遇?
(2)相遇处距出发点多远?
(3)相遇前甲乙两车的最大距离是多少?
解析:用a1表示甲车加速度,a2表示乙车加速度,根据图象上标明的数据可知:
a1=![]() =
=![]() m/s2,a2=
m/s2,a2=![]() =
=![]() m/s2.
m/s2.
(1)两车相遇表示它们通过的位移相等,设乙车运动t s后两车相遇,s1、s2分别表示它们的位移,则:
s2=![]() a2t2;s1=
a2t2;s1=![]() a1(t+2)2.
a1(t+2)2.
由于s1=s2,所以![]() a2t2=
a2t2=![]() a1(t+2)2
a1(t+2)2
将a1、a2值代入,整理得:
t2-4t-4=0
解得,t=2±2![]() .
.
t=-0.83 s(舍去),t=4.83 s.
(2)将t=2+2![]() 代入
代入
s2=![]() a2t2=
a2t2=![]() ×
×![]() ×(2+2
×(2+2![]() )2 m=17.48 m.
)2 m=17.48 m.
(3)在t=4 s以前甲车的速度大于乙车的速度,两车距离是逐渐增加的;t=4 s以后乙车的速度大于甲车的速度,它们之间距离是逐渐减小的,所以只有它们速度相等时距离才为最大.
Δs=s1-s2=![]() a1t2-
a1t2-![]() a2(t-2)2=
a2(t-2)2=![]() ×
×![]() ×42 m-
×42 m-![]() ×
×![]() ×22 m=3 m.
×22 m=3 m.
所以,它们在t=4 s时距离最大,为3 m.在图象中可以用△OPE与△CPE的面积之差来表示.
答案:(1)4.83 s (2)17.48 m (3)3 m

练习册系列答案
相关题目
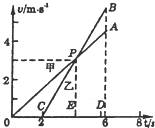 甲、乙两车从同一地点出发同向运动,其图象如图所示.试计算:
甲、乙两车从同一地点出发同向运动,其图象如图所示.试计算: 甲、乙两车从同一地点出发同向运动,其v-t图象如图所示.下列说法正确的是( )
甲、乙两车从同一地点出发同向运动,其v-t图象如图所示.下列说法正确的是( )