题目内容
“嫦娥一号”探月卫星沿地月转移轨道到达月球，在距月球表面200km的P点进行第一次“刹车制动”后被月球捕获，进入椭圆轨道Ⅰ绕月飞行，如图所示．之后，卫星在P点经过几次“刹车制动”，最终在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动．用T1、T2、T3分别表示卫星在椭圆轨道Ⅰ、Ⅱ和圆形轨道Ⅲ上运动的周期，用a1、a2、a3分别表示卫星沿三个轨道运动到P点的加速度，则下面说法正确的是（ ）
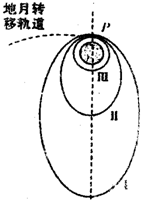
| A．a1＜a2＜a3 | B．T1＜T2＜T3 | C．T1＞T2＞T3 | D．a1＞a2＞a3 |
A、卫星从Ⅰ轨道的P处制动后进入Ⅱ轨道，在Ⅱ轨道的P处再制动，最后进入Ⅲ轨道．在不同轨道的P处，卫星受到的万有引力相同，根据牛顿第二定律可知加速度相同，A、D错误；
B、根据开普勒第三定律可知，卫星在不同轨道上绕月球运动时的周期的平方与轨道半长轴的三次方之比相同，显然Ⅰ轨道的半长轴最大，Ⅲ轨道的半径最小，故B错误，C正确．
故选C．
B、根据开普勒第三定律可知，卫星在不同轨道上绕月球运动时的周期的平方与轨道半长轴的三次方之比相同，显然Ⅰ轨道的半长轴最大，Ⅲ轨道的半径最小，故B错误，C正确．
故选C．
练习册系列答案
名题金卷系列答案
相关题目
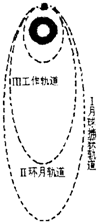2007年10月24日18时零5分，我国成功发射一颗探月卫星“嫦娥一号”．探月卫星绕地经过3次变轨飞行180多万公里，于2007年11月5日成功进入月球捕获轨道，如图I轨道；11月6日经第2次变轨进入环月轨道，如图II轨道；11月7日经第3次变轨进入工作轨道，如图9-III轨道．经过测试调整于2007年11月20日向地球发回首张照片，“嫦娥一号”成功发射在我国又掀起了新一轮航天热．关于“嫦娥一号”探月卫星，下列说法正确的是（ ）
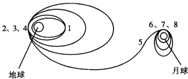2007年10月24日18时，我国成功发射了“嫦娥一号”探月卫星，卫星经过八次点火变轨后，绕月球做匀速圆周运动．图中所示为探月卫星运行轨迹的示意图（图中1、2、3、4、…、8为卫星运行中的八次点火位置），则下述说法正确的是（ ）