Question

（2011?崇明县二模）如图所示，绝缘轻杆长L=0.9m，两端分别固定着带等量异种电荷的小球A、B，质量分别为m_A=4×10^-2kg，m_B=8×10^-2kg，A球带正电，B球带负电，电荷量q=6.0×10^-6C．轻杆可绕过O点的光滑水平轴转动，OB=2OA．一根竖直细线系于杆上OB中点D使杆保持水平，整个装置处在水平向右的匀强电场中，电场强度E=5×10⁴N/C．不计一切阻力，取g=10m/s²，求：
（1）细线对杆的拉力大小；
（2）若将细线烧断，当轻杆转过90°时，A、B两小球电势能总的变化量；
（3）细线烧断后，在杆转动过程中小球A的最大速度．

Answer 1

分析：（1）正确对两小球进行受力分析，然后依据力矩平衡求解．
（2）根据功能关系可知，电场力做功对应着电势能的变化，因此根据电场力做功特点，求出当轻杆转过90°时，电场力对两球做功代数和即可．
（3）转动过程中AB两球速度之比为：v_A：v_B=1：2，且当力矩的代数和为零时，B球的速度达到最大，然后依据功能关系求解即可．

解答：解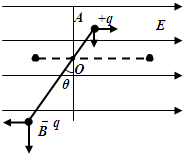：（1）根据有固定转动轴物体的平衡条件，有：
mAg

L

3

+T

L

3

=mBg

2L

3

T=（2m_B-m_A）g=1.2（N）
故细线对杆的拉力大小为1.2N
（2）杆转过90°时，电场力对两带电小球做正功，电势能减少，所以有：
△E=W=qAE

L

3

+qBE

2L

3

=qEL
代入数据得：△E=0.27（J）　　　　
故A、B两小球电势能总的变化量为0.27J．
（3）当力矩的代数和为零时，B球的速度达到最大，此时有：
mBg

2L

3

sinθ =mAg

L

3

sinθ+qE

2L

3

cosθ+qE

L

3

cosθ
所以有：tanθ=

3qE

(2mB-mA)g

=

3

4

故θ=37°　
由动能定理得：
mBg

2L

3

cosθ+qE

2L

3

(1+sinθ)+qE

L

3

(1+sinθ)-mAg

L

3

cosθ=

1

2

mA

v

2 A

+

1

2

mB

v

2 B

v_B=2v_A
联立求得：v_A=2m/s
故细线烧断后，在杆转动过程中小球A的最大速度为2m/s．

点评：本题考查了力矩平衡知识依据动能定理应用，考查知识点比较全面，学生容易出错，因此平时要加强这方面的训练．