题目内容
1.如图所示,某发电机输出功率是100kW,输出电压是250V,从发电机到用户间的输电线总电阻为8Ω,要使输电线上的功率损失为5%,而用户得到的电压正好为220V,求升压变压器和降压变压器原、副线圈匝数比分别是( )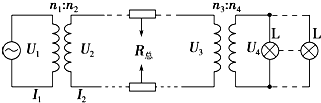
| A. | 16:1 190:11 | B. | 1:16 11:190 | C. | 1:16 190:11 | D. | 16:1 11:190 |
分析 发电机输出功率是100kW,输出电压是250V,根据P=UI可计算出升压变压器原线圈的输入电流I1,在根据输电线上的功率损失为5%,可计算出升压变压器副线圈的电流I2,根据 $\frac{{n}_{1}}{{n}_{2}}$=$\frac{{I}_{2}}{{I}_{1}}$ 即可求出升压变压器的匝数比;由题意可计算出用户得到的功率,根据P=UI又可计算出降压变压器原线圈两端的电压,根据$\frac{{U}_{3}}{{U}_{4}}$=$\frac{{n}_{3}}{{n}_{4}}$即可求出降压变压器的匝数比.
解答 解:输电线损失功率P损=100×103×5% W=5×103 W,
所以,输电线电流I2=$\sqrt{\frac{{P}_{损}}{{R}_{损}}}$=25 A,
升压变压器原线圈电流I1=$\frac{{P}_{总}}{{U}_{1}}$=400 A,
故升压变压器原、副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}=\frac{{I}_{2}}{{I}_{1}}$=$\frac{1}{16}$.
升压变压器副线圈端电压U2=$\frac{{n}_{2}}{{n}_{1}}$U1=4000 V,
输电线损失电压U损=I2R线=200 V,
降压变压器原线圈电压U3=U2-U损=3800 V,
故降压变压器原、副线圈匝数比为$\frac{{n}_{3}}{{n}_{4}}$=$\frac{{U}_{3}}{{U}_{4}}$=$\frac{190}{11}$.故C正确,ABD错误.
故选:C.
点评 解决本题的关键知道原副线圈的匝数比等于原副线圈的电压比,以及掌握输电线上损失的功率P损=I2R.输电线上损失的功率往往是突破口.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
16. 如图所示,木箱内竖直放置的弹簧上方有一物块,木箱静止时弹簧处于压缩状态且物块与箱顶间压力为F0,若在某一段时间内,物块与箱顶间的压力大于F0,则在这段时间内木箱的运动情况可能是( )
如图所示,木箱内竖直放置的弹簧上方有一物块,木箱静止时弹簧处于压缩状态且物块与箱顶间压力为F0,若在某一段时间内,物块与箱顶间的压力大于F0,则在这段时间内木箱的运动情况可能是( )
 如图所示,木箱内竖直放置的弹簧上方有一物块,木箱静止时弹簧处于压缩状态且物块与箱顶间压力为F0,若在某一段时间内,物块与箱顶间的压力大于F0,则在这段时间内木箱的运动情况可能是( )
如图所示,木箱内竖直放置的弹簧上方有一物块,木箱静止时弹簧处于压缩状态且物块与箱顶间压力为F0,若在某一段时间内,物块与箱顶间的压力大于F0,则在这段时间内木箱的运动情况可能是( )| A. | 加速下降 | B. | 加速上升 | C. | 减速下降 | D. | 减速上升 |
13.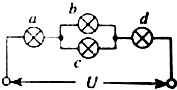 四盏灯泡接成如图所示的电路,a、c灯泡的规格为“220V 40W”,b、d灯泡的规格为“220V 100W”,各个灯泡的实际功率都没有超过它的额定功率,则四盏灯泡实际消耗功率的大小顺序是( )
四盏灯泡接成如图所示的电路,a、c灯泡的规格为“220V 40W”,b、d灯泡的规格为“220V 100W”,各个灯泡的实际功率都没有超过它的额定功率,则四盏灯泡实际消耗功率的大小顺序是( )
 四盏灯泡接成如图所示的电路,a、c灯泡的规格为“220V 40W”,b、d灯泡的规格为“220V 100W”,各个灯泡的实际功率都没有超过它的额定功率,则四盏灯泡实际消耗功率的大小顺序是( )
四盏灯泡接成如图所示的电路,a、c灯泡的规格为“220V 40W”,b、d灯泡的规格为“220V 100W”,各个灯泡的实际功率都没有超过它的额定功率,则四盏灯泡实际消耗功率的大小顺序是( )| A. | Pa>Pd>Pb>Pc | B. | Pc>Pb>Pd>Pa | C. | Pa>Pc>Pd>Pb | D. | Pb>Pc>Pa>Pd |
11.下列说法正确的是( )
| A. | 卢瑟福通过α粒子散射实验建立了原子核式结构模型 | |
| B. | β衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 | |
| C. | 爱因斯坦在对光电效应的研究中,提出了光子说 | |
| D. | 根据玻尔理论可知,氢原子辐射出一个光子后,氢原子的电势能增大,核外电子的运动动能减小 |
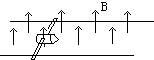 电磁炮是利用磁场对电流的作用力把电能转变成机械能,使炮弹发射出去.如图所示,把两根长为s(s足够大),互相平行的铜制轨道放在磁场中,轨道之间放有质量为m的炮弹,炮弹架在长为L、质量为M的金属架上,已知金属架与炮弹在运动过程中所受的总阻力与速度平方成正比,当有恒定的大电流I1通过轨道和炮弹架时,炮弹与金属架在磁场力的作用下,获得速度v1时刻加速度为a,当有恒定的大电流I2通过轨道和金属架时,炮弹最大速度为v2,则垂直于轨道平面的磁感应强度为多少?
电磁炮是利用磁场对电流的作用力把电能转变成机械能,使炮弹发射出去.如图所示,把两根长为s(s足够大),互相平行的铜制轨道放在磁场中,轨道之间放有质量为m的炮弹,炮弹架在长为L、质量为M的金属架上,已知金属架与炮弹在运动过程中所受的总阻力与速度平方成正比,当有恒定的大电流I1通过轨道和炮弹架时,炮弹与金属架在磁场力的作用下,获得速度v1时刻加速度为a,当有恒定的大电流I2通过轨道和金属架时,炮弹最大速度为v2,则垂直于轨道平面的磁感应强度为多少?

 在托乒乓球跑步比赛中,某同学将质量为m的球置于球拍光面中心,t=0时以大小为a的加速度从静止开始做匀加速直线运动,t=t0起做匀速直线运动,球始终保持在位于球拍中心不动.在运动过程中球受到与其速度方向相反、大小成正比的空气阻力,比例系数为k,运动中球拍拍面与水平方向夹角为θ.则匀速运动时tanθ=$\frac{ka{t}_{0}}{mg}$;匀加速直线运动过程中tanθ随时间t变化的关系式为tanθ=$\frac{a}{g}$+$\frac{kat}{mg}$.(不计球与球拍间的摩擦,重力加速度取g)
在托乒乓球跑步比赛中,某同学将质量为m的球置于球拍光面中心,t=0时以大小为a的加速度从静止开始做匀加速直线运动,t=t0起做匀速直线运动,球始终保持在位于球拍中心不动.在运动过程中球受到与其速度方向相反、大小成正比的空气阻力,比例系数为k,运动中球拍拍面与水平方向夹角为θ.则匀速运动时tanθ=$\frac{ka{t}_{0}}{mg}$;匀加速直线运动过程中tanθ随时间t变化的关系式为tanθ=$\frac{a}{g}$+$\frac{kat}{mg}$.(不计球与球拍间的摩擦,重力加速度取g)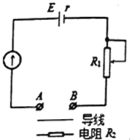 在如图所示的电路中,电源的电动势E=1.5V.内阻r=0.5Ω,电流表满偏电流Ig=10mA,电流表的电阻Rg=7.5Ω,A、B为接线柱.
在如图所示的电路中,电源的电动势E=1.5V.内阻r=0.5Ω,电流表满偏电流Ig=10mA,电流表的电阻Rg=7.5Ω,A、B为接线柱.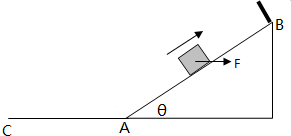 如图所示,粗糙斜面长L=5m,倾角θ=37°,在斜面顶端B处有一弹性挡板,质量m=0.5kg的物块从斜面的中点以v0=12m/s的速度沿斜面向上运动,同时施加一个水平向右的恒力F=10N,设物块与挡板碰撞前后速度大小不变,恒力始终存在.滑块和地面间及斜面间的动摩擦因数都是μ=0.1,g=10m/s2,(sin37°=0.6,cos37°=0.8)
如图所示,粗糙斜面长L=5m,倾角θ=37°,在斜面顶端B处有一弹性挡板,质量m=0.5kg的物块从斜面的中点以v0=12m/s的速度沿斜面向上运动,同时施加一个水平向右的恒力F=10N,设物块与挡板碰撞前后速度大小不变,恒力始终存在.滑块和地面间及斜面间的动摩擦因数都是μ=0.1,g=10m/s2,(sin37°=0.6,cos37°=0.8)