题目内容
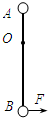
AB两个质量均为m的小球,被一轻杆AB固定,轻杆长AB=L,OA=L/3,杆可绕O点的水平轴无摩擦地转动,初始时杆静止在竖直位置,如图所示,今在B球上施加一水平方向恒力F=
mg,试求:
(1)转过90°过程中恒力做了多少功?
(2)在转动过程中B球获得的最大速度时AB杆与竖直方向夹角为多大?
(3)在转动过程中B球获得的最大速度是多少?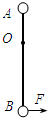
| ||
| 2 |
(1)转过90°过程中恒力做了多少功?
(2)在转动过程中B球获得的最大速度时AB杆与竖直方向夹角为多大?
(3)在转动过程中B球获得的最大速度是多少?

(1)W=FlOB=
mgL
(2)B球获得最大速度时,系统处于力矩平衡状态,设杆和竖直方向夹角为θ,应有:mg
sinθ+F
Lcosθ=mg
sinθ,
可得θ=60°;
(3)设B球最大速度为v,则此时A球的速度应为
,根据动能定理得:
F×
Lsinθ-mg
(1-cosθ)+mg
(1-cosθ)=
mv2+
m(
v)2,
解得:v=2
m/s.
答:(1)转过90°过程中恒力做功为
mgL;
(2)在转动过程中B球获得的最大速度时AB杆与竖直方向夹角为60°;
(3)在转动过程中B球获得的最大速度是2
m/s.
| ||
| 3 |
(2)B球获得最大速度时,系统处于力矩平衡状态,设杆和竖直方向夹角为θ,应有:mg
| L |
| 3 |
| 2 |
| 3 |
| 2L |
| 3 |
可得θ=60°;
(3)设B球最大速度为v,则此时A球的速度应为
| v |
| 2 |
F×
| 2 |
| 3 |
| 2L |
| 3 |
| L |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:v=2
|
答:(1)转过90°过程中恒力做功为
| ||
| 3 |
(2)在转动过程中B球获得的最大速度时AB杆与竖直方向夹角为60°;
(3)在转动过程中B球获得的最大速度是2
|

练习册系列答案
相关题目
 (2011?普陀区二模)AB两个质量均为m的小球,被一轻杆AB固定,轻杆长AB=L,OA=L/3,杆可绕O点的水平轴无摩擦地转动,初始时杆静止在竖直位置,如图所示,今在B球上施加一水平方向恒力F=
(2011?普陀区二模)AB两个质量均为m的小球,被一轻杆AB固定,轻杆长AB=L,OA=L/3,杆可绕O点的水平轴无摩擦地转动,初始时杆静止在竖直位置,如图所示,今在B球上施加一水平方向恒力F=
 mg,试求:
mg,试求:
 mg,试求:
mg,试求: