题目内容
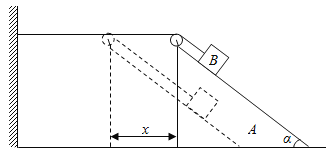
【题目】两物体A、B静止于水平地面上,A物体的质量为m,B物体的质量为3m,物体A与地面间的动摩擦因数μ=0.2,如图所示.对A物体施加向右的瞬时冲量,使其获得v0=4m/s的初速度,经时间t=1s,物体A与B发生弹性碰撞.求:
![]()
(1)物体A与B碰撞前的速度大小v1;
(2)碰撞后物体A的滑行距离.
【答案】(1) v1=2m/s (2) x=0.25m
【解析】试题分析:物体A与B碰撞前受重力、支持力和滑动摩擦力,做匀减速直线运动,根据牛顿第二定律求解加速度,根据速度时间关系公式列式求解与B碰撞前的速度;物体A与B发生弹性碰撞,根据动量守恒定律和机械能守恒定律列式后联立求解得到A的碰撞后速度;然后根据动能定理列式求解继续滑行距离
(1)物体A与B碰撞前受重力、支持力和滑动摩擦力
根据牛顿第二定律,有:F合=-μmg=ma
解得:a=-μg=-2m/s2
物体A与B碰撞前的速度大小:v1=v0+at=4-2×1=2m/s
(2)物体A与B发生弹性碰撞
根据动量守恒定律:![]()
根据机械能守恒定律: ![]()
![]()
联立解得:![]()
![]() (不合实际,后面的物体的速度不可能大于前面物体的速度)
(不合实际,后面的物体的速度不可能大于前面物体的速度)
或者![]()
![]()
即物体A以1m/s的速度反弹,此后向左做匀减速直线运动,根据动能定理,有:
![]()
解得:x=0.25m

练习册系列答案
相关题目