题目内容
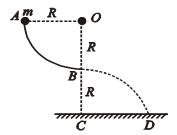
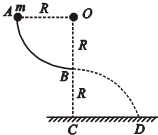 如图所示,AB是粗糙的
如图所示,AB是粗糙的| 1 | 4 |
①小球经过B点时,对轨道的压力?
②小球在AB段克服阻力做的功?
分析:(1)从球从B→D做平抛运动,已知水平位移和竖直方向的位移,根据平抛运动的运动规律即可求得B点的速度.
(2)小球从A→B,做圆周运动,受到重力、轨道的支持力和摩擦力,支持力不做功,根据动能定理即可求得小球克服阻力做的功.
(2)小球从A→B,做圆周运动,受到重力、轨道的支持力和摩擦力,支持力不做功,根据动能定理即可求得小球克服阻力做的功.
解答: 解:①B到D小球做平抛运动
解:①B到D小球做平抛运动
解得vB=
B点小球受重力和支持力的合力提供向心力,
有牛顿第二定律得
解得 N=
mg
由牛顿第三定律,小球对轨道的压力N′=
mg,竖直向下
②小球从A到B的过程中,由动能定理得:
解得;
=-
mgR
即小球克服阻力做功为
mgR
答:小球经过B点时,对轨道的压力为
mg,方向竖直向下;小球在AB段克服阻力做的功为
mgR.
 解:①B到D小球做平抛运动
解:①B到D小球做平抛运动
|
解得vB=
|
B点小球受重力和支持力的合力提供向心力,
有牛顿第二定律得
|
解得 N=
| 3 |
| 2 |
由牛顿第三定律,小球对轨道的压力N′=
| 3 |
| 2 |
②小球从A到B的过程中,由动能定理得:
|
解得;
|
| 3 |
| 4 |
即小球克服阻力做功为
| 3 |
| 4 |
答:小球经过B点时,对轨道的压力为
| 3 |
| 2 |
| 3 |
| 4 |
点评:本题是牛顿定律、平抛运动和动能定理等知识的综合应用,比较简单.但对于第(1)要特别注意求得是小球对轨道的压力,应用牛顿第三定律转换过来.

练习册系列答案
相关题目
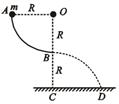
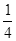 圆弧,半径为R,OA水平,OB竖直,O点离地面高度为2R,一质量为m的小球,从A点静止释放,不计空气阻力,最后落在距C点R处的D点。求:
圆弧,半径为R,OA水平,OB竖直,O点离地面高度为2R,一质量为m的小球,从A点静止释放,不计空气阻力,最后落在距C点R处的D点。求: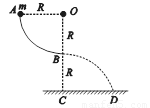
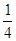 圆弧,半径为R,OA水平,OB竖直,O点离地面高度为2R,一质量为m的小球,从A点静止释放,不计空气阻力,最后落在距C点R处的D点。
圆弧,半径为R,OA水平,OB竖直,O点离地面高度为2R,一质量为m的小球,从A点静止释放,不计空气阻力,最后落在距C点R处的D点。