题目内容
质量为6㎏的物体，静止于水平方桌面上，物体与桌面之间的动摩擦因数为μ=0.5，一跟水平方向成仰角53°的力F作用于物体上，使其加速运动，试求：
（1）物体在水平面上作加速运动而不脱离桌面时，力F的取值范围？
（2）力F取何值时，物体在水平面上的加速度最大？最大加速度值为多少？
（sin53°°=0.8，cos53°=0.6，g=10m/s2）
解：（1）欲使物体不离开桌面则：
Fsin53°≤mg
解得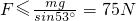
．
欲使物体在水平面上做加速运动，则：
Fsin53°+N=mg
Fcos53°-μN＞0
解得：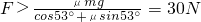
故 30N＜F≤75N
（2）设力为F时，物体的加速度为a，则
Fsin53°+N=mg
Fcos53°-μN=ma
解得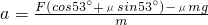
故F=75N时，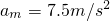
．
答：（1）物体在水平面上作加速运动而不脱离桌面时，力F的取值范围为30N＜F≤75N
（2）当F=75N时，物体的加速度最大，最大为7.5m/s2．
分析：（1）物块不脱离桌面，则F的竖直方向上的分力小于等于mg，做加速运动，则F水平方向上的分力大于摩擦力．根据两个关系求出F的取值范围．
（2）根据牛顿第二定律，通过正交分解求出加速度，得出F最大时，加速度最大．
点评：解决本题的关键能够正确地受力分析，运用牛顿第二定律进行求解．注意正交分解法的运用．
Fsin53°≤mg
解得
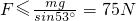．欲使物体在水平面上做加速运动，则：
Fsin53°+N=mg
Fcos53°-μN＞0
解得：
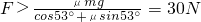
故 30N＜F≤75N
（2）设力为F时，物体的加速度为a，则
Fsin53°+N=mg
Fcos53°-μN=ma
解得
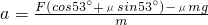
故F=75N时，
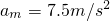．答：（1）物体在水平面上作加速运动而不脱离桌面时，力F的取值范围为30N＜F≤75N
（2）当F=75N时，物体的加速度最大，最大为7.5m/s2．
分析：（1）物块不脱离桌面，则F的竖直方向上的分力小于等于mg，做加速运动，则F水平方向上的分力大于摩擦力．根据两个关系求出F的取值范围．
（2）根据牛顿第二定律，通过正交分解求出加速度，得出F最大时，加速度最大．
点评：解决本题的关键能够正确地受力分析，运用牛顿第二定律进行求解．注意正交分解法的运用．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，在倾角为37°的固定斜面上静置一个质量为5kg的物体，物体与斜面间的动摩擦因数为0.8．求：
质量为M，倾角为θ的直角劈静置于光滑水平地面上．质量为m的物体放在劈的斜面上，如图序所示，设M=2.0kg，m=1.0kg，θ=37．物体与劈面间的动摩擦因数μ=0.25．