题目内容
18．
矩形导线框abcd固定在匀强磁场中（如图甲），磁感线的方向与导线框所在平面垂直，规定磁场的正方向垂直纸面向里，磁感应强度B随时间t变化的规律如图乙，则（ ）| A． | 从0到t1时间内，导线框中电流越来越小 | |
| B． | 从0到t1时间内，导线框中电流的方向为adcba | |
| C． | 从t1到t2时间内，导线框中电流越来越大 | |
| D． | 从t1到t2时间内，导线框bc边受到安培力大小保持不变 |
分析 由右图可知B的变化，则可得出磁通量的变化情况，由楞次定律可知电流的方向；由法拉第电磁感应定律可知电动势，即可知电路中电流的变化情况；由F=BIL可知安培力的变化情况．
解答 解：A、从0到t1时间内，线圈中磁通量的变化率相同，由E=$\frac{△B•S}{△t}$可知，电路中电流大小时恒定不变；同理从t1到t2时间内，导线电流大小恒定，故AC错误；
B、由图可知，0-t1内，线圈中磁通量的变化率相同，故0到t1时间内电流的方向相同，由楞次定律可知，电路中电流方向为顺时针，即电流为adcba方向，故B正确；
D、从t1到t2时间内，电路中电流大小时恒定不变，故由F=BIL可知，F与B成正比，故D错误；
故选：B．
点评 本题要求学生能正确理解B-t图的含义，才能准确的利用楞次定律、左手定律等进行判定；解题时要特别注意，两个时段，虽然磁场的方向发生了变化，但因其变化为连续的，故产生的电流一定是相同的．
练习册系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
相关题目
5．
如图所示，在竖直平面内有匀强电场（图中未画出），一个质量为m带电小球，从A点以初速度v0沿直线运动．直线与竖直方向的夹角为θ（θ＜90°），不计空气阻力，重力加速度为g．以下说法正确的是（ ）
如图所示，在竖直平面内有匀强电场（图中未画出），一个质量为m带电小球，从A点以初速度v0沿直线运动．直线与竖直方向的夹角为θ（θ＜90°），不计空气阻力，重力加速度为g．以下说法正确的是（ ）| A． | 小球一定做匀变速运动 | |
| B． | 小球在运动过程中可能机械能守恒 | |
| C． | 当小球速度为v时，其重力的瞬时功率p=mgvsinθ | |
| D． | 小球运动过程中所受电场力不小于mgsinθ |
9．简谐运动的图象的横坐标和纵坐标分别表示运动物体的（ ）
| A． | 时间t，振幅A | B． | 时间t，对平衡位置的位移x | ||
| C． | 对平衡位置的位移x，时间t | D． | 时间t，周期T |
6．
如图所示，杆BC的B端用铰链接在竖直墙上，另一端C为一滑轮．重物G上系一绳经过滑轮固定于墙上A点处，杆恰好平衡．若将绳的A端沿墙缓慢向下移（BC杆、滑轮、绳的质量及摩擦均不计），则（ ）
如图所示，杆BC的B端用铰链接在竖直墙上，另一端C为一滑轮．重物G上系一绳经过滑轮固定于墙上A点处，杆恰好平衡．若将绳的A端沿墙缓慢向下移（BC杆、滑轮、绳的质量及摩擦均不计），则（ ）| A． | 绳的拉力增大，BC杆受绳的压力增大 | |
| B． | 绳的拉力不变，BC杆受绳的压力增大 | |
| C． | 绳的拉力不变，BC杆受绳的压力减小 | |
| D． | 绳的拉力不变，BC杆受绳的压力不变 |
13．
放在粗糙水平面上的物块A、B用轻质弹簧秤相连，如图所示，物块与水平间的动摩擦因数均为μ，今对物块A施加一水平向左的恒力F、使A、B一起向左匀加速运动，设A、B的质量分别为m、M，则弹簧秤的示数为（ ）
放在粗糙水平面上的物块A、B用轻质弹簧秤相连，如图所示，物块与水平间的动摩擦因数均为μ，今对物块A施加一水平向左的恒力F、使A、B一起向左匀加速运动，设A、B的质量分别为m、M，则弹簧秤的示数为（ ）| A． | $\frac{M}{m}$F | B． | $\frac{M}{M+m}$F | C． | $\frac{F-μ（M+m）g}{m}M$ | D． | $\frac{F-μ（M+m）g}{M+m}M$ |
3．
某同学在做“探究弹力和弹簧伸长量的关系”的实验，所用实验装置如图所示，所用的钩码每只质量都是30g，他先测出不挂钩吗时的弹簧的自然长度，再将5个钩码逐个挂在弹簧的下端，每次都测出相应的弹簧总长度，并将数据填在表中，实验中弹簧始终未超过弹性限度，取g=10m/s2，则：
（1）试根据这些实验数据在如图2所示的坐标系中作出弹簧弹力大小与弹簧总长度之间的函数关系的图线．
（2）该弹簧的劲度系数k=25.9N/m（计算结果保留两位有效数字）．
某同学在做“探究弹力和弹簧伸长量的关系”的实验，所用实验装置如图所示，所用的钩码每只质量都是30g，他先测出不挂钩吗时的弹簧的自然长度，再将5个钩码逐个挂在弹簧的下端，每次都测出相应的弹簧总长度，并将数据填在表中，实验中弹簧始终未超过弹性限度，取g=10m/s2，则：| 钩码质量（g） | 0 | 30 | 60 | 90 | 120 | 150 |
| 弹簧总长（cm） | 6.00 | 7.00 | 8.00 | 9.00 | 10.00 | 11.00 |
（2）该弹簧的劲度系数k=25.9N/m（计算结果保留两位有效数字）．
如图所示，M为一线圈电阻rM=0.4Ω的电动机，R=24Ω，电源电动势E=40V．当S断开时，电流表的示数为I1=1.6A，当开关S闭合时，电流表的示数为I2=4.0A．求：
8．
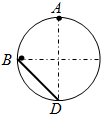如图所示，将小球甲、乙（都可视为质点）分别从A、B两点由静止同时释放，最后都到达竖直面内圆弧的最低点D，其中甲是从A出发做自由落体运动，乙沿弦轨道从一端B到达另一端D．如果忽略一切摩擦阻力，那么下列判断正确的是（ ）
如图所示，将小球甲、乙（都可视为质点）分别从A、B两点由静止同时释放，最后都到达竖直面内圆弧的最低点D，其中甲是从A出发做自由落体运动，乙沿弦轨道从一端B到达另一端D．如果忽略一切摩擦阻力，那么下列判断正确的是（ ）| A． | 甲、乙同时到达D点 | B． | 甲球最先到达D点 | ||
| C． | 乙球最先到达D点 | D． | 无法判断哪个球先到达D点 |