题目内容
16.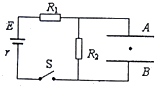 如图所示的电路中,两平行金属板A,B水平放置,接入如图所示电路中,两板间的距离d=50cm,电源电动势E=15V,内电阻r,电阻R1=4Ω,R2=10Ω,闭合开关S,待电路稳定后,将一带电的小球放入板间恰能保持静止,若小球质量为m=2×10-2kg,电量q=1×10-2C,问:
如图所示的电路中,两平行金属板A,B水平放置,接入如图所示电路中,两板间的距离d=50cm,电源电动势E=15V,内电阻r,电阻R1=4Ω,R2=10Ω,闭合开关S,待电路稳定后,将一带电的小球放入板间恰能保持静止,若小球质量为m=2×10-2kg,电量q=1×10-2C,问:(1)小球带正电还是负电,电容器的电压为多大?
(2)电源的内阻为多大?
(3)电源的效率是多大?(取g=10m/s2)
分析 (1)小球放入板间后,受重力和电场力作用,由二力平衡判断电场力的方向,进而判断电荷的正负,根据受力平衡求解电容器电压;
(2)由欧姆定律求出通过电路的电流,再根据闭合电路欧姆定律求解内阻;
(3)根据$η=\frac{UI}{EI}×100%%$求解电源效率.
解答 解:(1)小球放入板间后,受重力和电场力作用,由二力平衡,小球应带负电,且$mg=\frac{{U}_{2}}{d}q$,
解得:${U}_{2}=\frac{mgd}{q}=\frac{2×1{0}^{-2}×10×0.5}{1×1{0}^{-2}}=10V$,
(2)电路中的电流I=$\frac{{U}_{2}}{{R}_{2}}=\frac{10}{10}=1A$
根据闭合电路欧姆定律得:
E=U2+I(R1+r)
解得:r=$\frac{15-10}{1}-4=1Ω$
(3)电源的效率$η=\frac{UI}{EI}×100%=\frac{{U}_{1}+{U}_{2}}{E}×100%=\frac{4+10}{15}$×100%=93.33%
答:(1)小球带负电,电容器的电压为10V;
(2)电源的内阻为1Ω;
(3)电源的效率是93.33%.
点评 本题关键是分析清楚电路结构和运动情况后,根据平衡条件、欧姆定律联立列式求解,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.kg和s是国际单位制两个基本单位的符号,这两个基本单位对应的物理量是( )
| A. | 质量和时间 | B. | 质量和位移 | C. | 重力和时间 | D. | 重力和位移 |
7.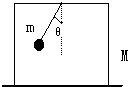 如图一个箱子放在水平地面上,质量为M,箱内用一长为L的细线拴一小球,绳的另一端拴在箱子的顶板上,小球质量为m现把细绳拉到与竖直方向成θ角自由释放,当球摆到最低点时,地面受到的压力为( )
如图一个箱子放在水平地面上,质量为M,箱内用一长为L的细线拴一小球,绳的另一端拴在箱子的顶板上,小球质量为m现把细绳拉到与竖直方向成θ角自由释放,当球摆到最低点时,地面受到的压力为( )
 如图一个箱子放在水平地面上,质量为M,箱内用一长为L的细线拴一小球,绳的另一端拴在箱子的顶板上,小球质量为m现把细绳拉到与竖直方向成θ角自由释放,当球摆到最低点时,地面受到的压力为( )
如图一个箱子放在水平地面上,质量为M,箱内用一长为L的细线拴一小球,绳的另一端拴在箱子的顶板上,小球质量为m现把细绳拉到与竖直方向成θ角自由释放,当球摆到最低点时,地面受到的压力为( )| A. | mg(3-2cosθ) | B. | Mg+2mg(1-cosθ) | C. | (M+m)g | D. | Mg+mg(3-2cosθ) |
11. 如图所示,电源电动势为E,内阻r,R1为定值电阻,在滑动变阻器R2的滑片p向右移动时,则以下说法正确的是( )
如图所示,电源电动势为E,内阻r,R1为定值电阻,在滑动变阻器R2的滑片p向右移动时,则以下说法正确的是( )
 如图所示,电源电动势为E,内阻r,R1为定值电阻,在滑动变阻器R2的滑片p向右移动时,则以下说法正确的是( )
如图所示,电源电动势为E,内阻r,R1为定值电阻,在滑动变阻器R2的滑片p向右移动时,则以下说法正确的是( )| A. | 电源的总功率一定减小 | B. | 电源的效率先增大后减小 | ||
| C. | 当R2=R1+r时,R2消耗的功率最大 | D. | 当R1=R2+r时,R1消耗的功率最大 |
1.某电解池,如果在2秒钟内共有1.0×1019个二价正离子和2.0×1019个一价负离子通过某横截面,那么通过这个横截面的电流是( )
| A. | 0 | B. | 1.6A | C. | 2.4A | D. | 3.2A |
8.如为一物体沿直线运动的速度图象,由此可知( )
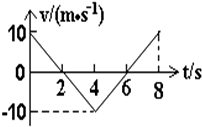

| A. | 8s内物体的位移为零 | B. | 4s末物体运动方向改变 | ||
| C. | 3s末与5s的加速度相等 | D. | 4s末与8s末物体处于同一位置 |
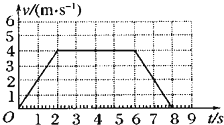 如图所示为某一质点的速度图象,求:
如图所示为某一质点的速度图象,求: