题目内容
 一物体在粗糙的水平面上做直线运动,运动速度v及所受水平拉力F随时间变化的图线如图所示,由此可知0-2s内拉力对物体所做的功为W=
一物体在粗糙的水平面上做直线运动,运动速度v及所受水平拉力F随时间变化的图线如图所示,由此可知0-2s内拉力对物体所做的功为W=40
40
J,物体与地面间的动摩擦因数为μ=0.3
0.3
.分析:根据速度时间图线求出0-2s内的位移,结合功的公式求出拉力对物体所做的功.根据0-2s内物体做匀减速直线运动,2-4s内做匀速直线运动,结合牛顿第二定律求出动摩擦因数的大小.
解答:解:在0-2s内,物体的位移:x=
×2m=8m
物体做匀减速直线运动的加速度大小:a=
m/s2=2m/s2.
则拉力做功:W=Fx=5×8J=40J.
匀速运动时,拉力等于摩擦力,f=15N.
在0-2s内,f-F=ma,解得:m=
=
kg=5kg.
则动摩擦因数:μ=
=
=0.3.
故答案为:40,0.3.
| 6+2 |
| 2 |
物体做匀减速直线运动的加速度大小:a=
| 6-2 |
| 2 |
则拉力做功:W=Fx=5×8J=40J.
匀速运动时,拉力等于摩擦力,f=15N.
在0-2s内,f-F=ma,解得:m=
| f-F |
| a |
| 15-5 |
| 2 |
则动摩擦因数:μ=
| f |
| mg |
| 15 |
| 50 |
故答案为:40,0.3.
点评:本题考查了牛顿第二定律和图象的综合运用,知道速度时间图线与时间轴围成的面积表示位移,图线的斜率表示加速度.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
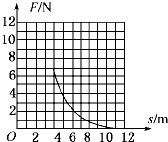 一质量为2kg的物体,在水平恒定拉力的作用下以某一速度在粗糙的水平面上做匀速运动,当运动一段时间后,拉力逐渐减小,且当拉力减小到零时,物体刚好停止运动,图中给出了拉力随位移的变化的关系图象.则根据以上信息可以精确得出或估算得出的物理量有( )
一质量为2kg的物体,在水平恒定拉力的作用下以某一速度在粗糙的水平面上做匀速运动,当运动一段时间后,拉力逐渐减小,且当拉力减小到零时,物体刚好停止运动,图中给出了拉力随位移的变化的关系图象.则根据以上信息可以精确得出或估算得出的物理量有( )| A、物体与水平面间的动摩擦因数 | B、合外力对物体做的功 | C、物体匀速运动时的速度 | D、物体运动的时间 |
 如图,斜面体A停放在粗糙的水平面内,滑块B被一沿斜面向上的力F作用沿斜面以速度v0匀速运动,某时刻突然撤除该外力F,下列说法正确的是( )
如图,斜面体A停放在粗糙的水平面内,滑块B被一沿斜面向上的力F作用沿斜面以速度v0匀速运动,某时刻突然撤除该外力F,下列说法正确的是( )| A、水平面对斜面体的支持力突然增大 | B、水平面对斜面体的摩擦力突然增大 | C、B物体对斜面体的作用力突然增大 | D、B物体所受的合外力突然增大 |
 如图所示,物体A的质量为m,A的右端连接一个轻弹簧,弹簧原长为L0,劲度系数为k,物体A静止在粗糙的水平面地面上,与地面间的动摩擦系数为μ,A与地面间的最大静摩擦力可以按滑动摩擦力计算,现将弹簧的右端点B缓慢地向右拉动,使B点向右移动,移动的距离为L,此时,物体A也在地面上移动了一段距离,则下列说法正确的是( )
如图所示,物体A的质量为m,A的右端连接一个轻弹簧,弹簧原长为L0,劲度系数为k,物体A静止在粗糙的水平面地面上,与地面间的动摩擦系数为μ,A与地面间的最大静摩擦力可以按滑动摩擦力计算,现将弹簧的右端点B缓慢地向右拉动,使B点向右移动,移动的距离为L,此时,物体A也在地面上移动了一段距离,则下列说法正确的是( )