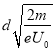题目内容
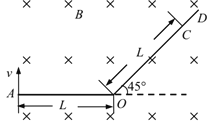
【题目】如图所示,地面某处有一粒子发射器A,发射器尺寸忽略不计,可以竖直向上发射速度介于v0~2v0的电子。发射器右侧距离A为L的O处,有一足够长突光板OD,可绕O点 转动,使其与水平方向的夹角![]() 可调,且AOD在同一平面内,其中OC段长度也为L, 电子打到荧光板上时,可使荧光板发光。在电子运动的范围内,加上垂直纸面向里的匀 强磁场。设电子质量为m,电荷量为e,重力忽略不计。初始
可调,且AOD在同一平面内,其中OC段长度也为L, 电子打到荧光板上时,可使荧光板发光。在电子运动的范围内,加上垂直纸面向里的匀 强磁场。设电子质量为m,电荷量为e,重力忽略不计。初始![]() =45°,若速度为2v0的电子恰好垂直打在荧光板上C点,求:
=45°,若速度为2v0的电子恰好垂直打在荧光板上C点,求:
(1)磁场的磁感应强度大小B;
(2)此时速率为1.5v0的电子打到荧光板上的位置到0点的距离x;
(3)在单位时间内发射器A发射N个电子,保持磁感应强度B不变,若打在荧光板上的电子数随速率均匀分布,且50%被板吸收,50%被反向弹回,弹回速率大小为打板前速率大小的0.5倍,求荧光板受到的平均作用力大小(只考虑电子与收集板的一次碰撞);
(4)若磁感应强度在(B-△B)到(B+△B)之间小幅波动,将荧光板![]() 角调整到90°,要在探测板上完全分辨出速度为v0和2v0的两类电子,则
角调整到90°,要在探测板上完全分辨出速度为v0和2v0的两类电子,则![]() 的最大值为多少?
的最大值为多少?
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]() (4)
(4)![]()
【解析】
(1)由洛伦兹力提供向心力:
qvB=m![]()
2v0对应半径为L,得
B=![]()
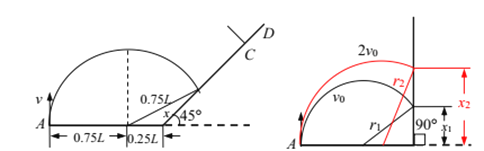
(2) 1.5v0对应运动半径为0.75L
cosl35°=![]()
![]()
解得:
x=![]()
取
x=![]()
(3)
F吸=![]()
F反=![]()
F总=F吸+F反=![]()
(4)
x1=![]()
x2=![]()
r1=![]()
r2=![]()
x2>x1
得![]() 最大值为
最大值为![]()

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目