题目内容
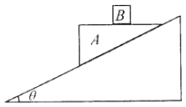
【题目】地面上固定一个倾角为θ的斜面体,在其光滑斜面上放置一质量为M上表面水平的三角形木块A,在三角形木块的上表面放置一个质量为m的木块B,它们一起沿斜面无相对滑动下滑,重力加速度为g。下列说法正确的是( )
A.A的加速度大小为![]() B.B受到沿斜面方向向上的摩擦力
B.B受到沿斜面方向向上的摩擦力
C.B受到的摩擦力大小为mgsinθcosθD.B受到的支持力大小为mgsin2θ
【答案】C
【解析】
A.对AB整体受力分析,由牛顿第二定律得:
(M+m)gsinθ=(M+m)a
解得:
a=gsinθ
故A错误;
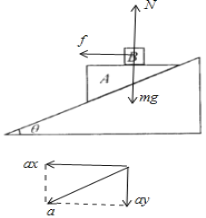
BCD.对B受力分析,将加速度分解,如图所示,
水平方向由牛顿第二定律得:
f=max
竖直方向由牛顿第二定律得:
mg﹣N=may
又
ax=acosθ ay=asinθ
联立解得:
f=mgsinθcosθ
N=mgcos2θ
故BD错误,C正确。
故选:C。

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目